Владимир Живетин - Системы аэромеханического контроля критических состояний

3) динамический: р ( · ) ≠ 0; .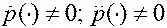

В стационарном режиме полета коэффициент подъемной силы С у в сечении Z по размаху крыла записывается в виде:

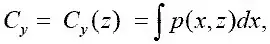
выделяют критический режим полета, например при C у > C усв.

В квазистационарном режиме полета,

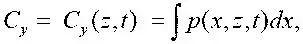
выделяют критический режим полета, например при C у > C у ( n укр ).

В динамическом режиме полета,

C у = C у ( z ,ω x ,,ω у ,ω z ,…),

выделяют критический режим полета, например при пространственном маневре.

Проблема состоит в упрощении математической модели самолета (1.10) без потери точности. Одним из важнейших путей является переход от системы с распределенными параметрами к системе с квазираспределенными, например к C у ( z ), где z – сечение по размаху несущей поверхности. Преимущество такого подхода: возможность построения Ω доп ( n y , V, α, V фл ) в процессе полета на всех режимах, где V фл – скорость флаттера крыла самолета.

Рассмотрим примеры в качестве иллюстрации сказанного.

1. Если при кренении во время полета угловая скорость ω x направлена в одну сторону, а увеличение Δ C y = C y пр – C y лев – в другую, то начался хаос, нет регулярной динамики, и управление необходимо формировать согласно не общим закономерностям, а с учетом особенностей обтекания. Так, например, в обратную сторону при штопоре, когда необходимо нейтрализовать вращение.

2. Скос потока от крыла на оперении. Необходимо учитывать запаздывание в образовании на оперении скоса потока. Как правило, запаздывание происходит в образовании подъемной силы на горизонтальном оперении, создаваемой вертикальными порывами, по сравнению с образованием ее на крыле.

3. Динамика изменения ПС АД p ( · ) обусловливает динамику нагрузок на конструкцию. Так, в момент входа в вертикальный порыв ветра (предполагая, что нестационарность обтекания крыла отсутствует) p ( · ) максимально возрастает, затем уменьшается за счет появления вертикальной скорости у самолета.

4. При возрастании числа Маха от 0 до 1 при входе крыла в вертикальный порыв ветра ( W у = 12 м/с) величина р ( · ) возрастает примерно в четыре раза.

Приведем некоторые модели приближенного описания изменения параметров ПС АД и зависимость его от параметров возмущенного движения [4]. В случае, когда исследуется крыло бесконечного размаха, движущееся с постоянной скоростью V, можно ограничиться рассмотрением профиля крыла в двумерном потоке.

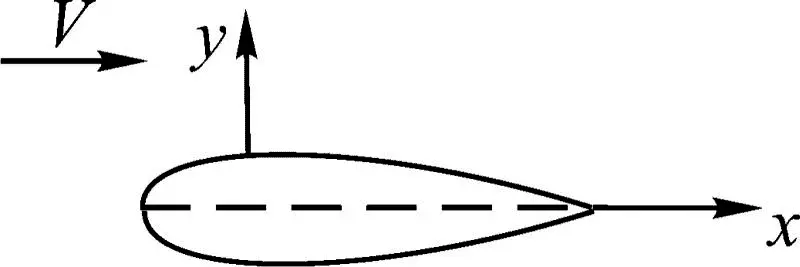
Рис. 1.10

Пусть профиль (рис. 1.10) совершает вертикальные перемещения y ( x,t ). При этом скорость потока нормальная к профилю:

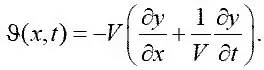
В каждой точке профиля формируется местный угол атаки:

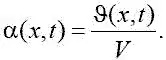
Если y ( x,t ) = y ( t ) + ( x 0– x )φ( t ), т. е. произвольная точка, отстоящая от носка профиля на величину х 0, перемещается на у ( t ) и поворачивается на угол φ( t ) относительно х 0, получим [21]:

– для подъемной силы сечения крыла

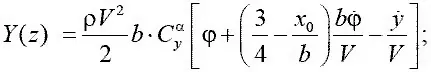
– для момента сечения крыла

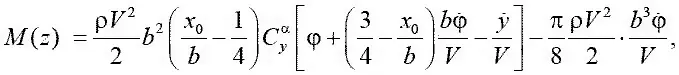
где b = b ( z ) – хорда крыла в сечении Z .

В случае если поток воздуха сверхзвуковой ( M > 1), а крыло совершает колебания с частотой ω, то приращение подъемной силы на единицу длины профиля Δ p ( x, t ) имеет вид:

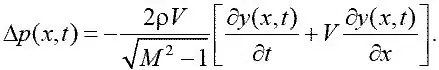
Тогда для подъемной силы

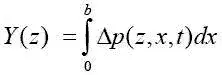
и момента M ( z ) получим:

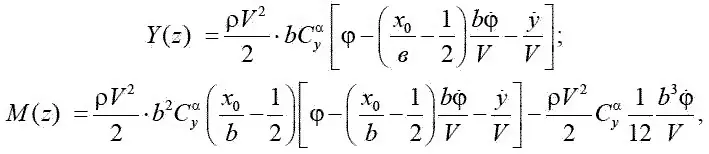
где C α у – экспериментальное значение производной, равной ∂ C у/ ∂α.

Пусть на крыле в точке с координатой (ξ,η) местный угол атаки равен α(ξ,η), за счет которого создается приращение давления Δ р ( х,z, ξ,η) в некоторой области Σ, которая зависит от режима обтекания и при M > 1 определяется конусом Маха с вершиной в точке (ξ,η) (рис. 1.11).

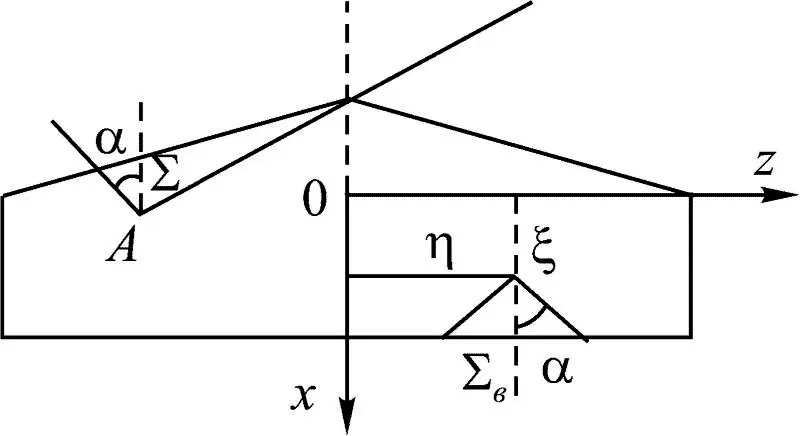
Рис. 1.11

Тогда

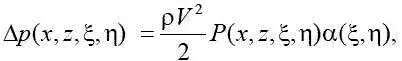
где P ( х,z ,ξ,η) – функция аэродинамического влияния, значение которой при фиксированных ( х,z ,ξ,η) равно аэродинамическим коэффициентам влияния.

Если известны α(ξ,η), тогда для давления в произвольной точке крыла с координатами ( x,z ) получим

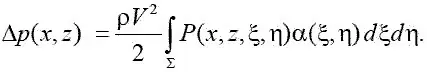
Здесь область интегрирования Σ включает то, что ограничено передним конусом Маха с вершиной в точке A ( x,z ).

Если перемещения y ( z,x,t ) заданы, то

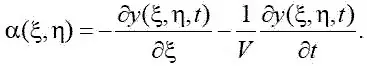
При этих условиях получим

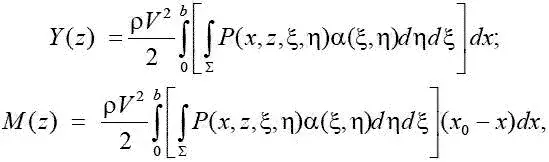
где b – хорда крыла в сечении z .

Рассмотрим скользящее крыло, расположенное под углом χ к набегающему потоку при M > 1. Исходное соотношение:

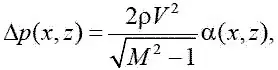
где α( x,z ) – местный угол, который справедлив при M → ∞.

Приближенное значение Δ р ( х,z ), когда задано перемещение y ( z,t ), имеет вид

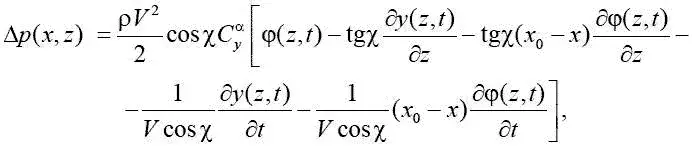
отсюда следует

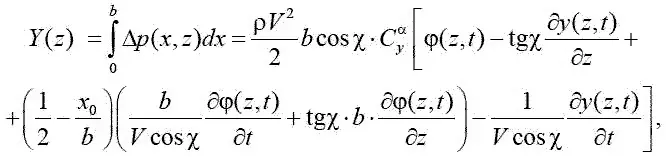
где φ( z,t ) – угол поворота сечения крыла.