Владимир Живетин - Системы аэромеханического контроля критических состояний

Асимметрия расположения областей срыва потока по крылу, обусловленная ω х , в свою очередь способствует дальнейшему увеличению абсолютной величины ω х .

Важная роль в возникновении срывного обтекания принадлежит геометрической и жесткостной асимметрии крыла, что способствует дополнительному изменению ПСАД, обусловливающему кренение самолета. При этом, когда α достигает α св , создаются условия для пространственного движения крена и тангажа большой амплитуды. Несимметричное зарождение и развитие областей срыва потока на крыле большей стреловидности и малого удлинения происходит с большой скоростью распространения срыва, что обусловливает появление сравнительно больших кренящих, а также заворачивающих аэродинамических моментов. Все это обусловлено перераспределением R y и R х .

На ПСАД при сваливании с некоординированных маневров при большой приборной скорости и числах М важную роль оказывают асимметрия, неравномерность и нестабильность обтекания самолета на исходном режиме (β 0≠ 0, ω x 0≠ 0, ω y 0≠ 0). При таком режиме уменьшается результирующая аэродинамическая сила R и ее вертикальная составляющая R y . При β 0≠ 0 возникает скольжение, например, на левое крыло, что уменьшает эффективный угол стреловидности этого крыла и увеличивает его подъемную силу. Это приводит к изменению направления вращения.

Определяющая роль принадлежит коэффициенту подъемной силы C y в силу его зависимости не только от α, но и от χ, M , β, ω, где χ – угол стреловидности крыла. В итоге мы можем констатировать, что законы образования аэродинамических сил и моментов в статике плоского движения и динамике пространственного движения изменяются. В этой ситуации информация об α для формирования управления, в том числе ограничения критических состояний, не имеет смысла. Здесь необходимо использовать информацию о величине C y (·).

Рассмотрим функции C y (·) на качественном уровне. На рис. 1.17 приведены функции C у (α) для стреловидного крыла (2), прямого (1) и соответствующие этим функциям критические значения угла атаки α кр крыла.

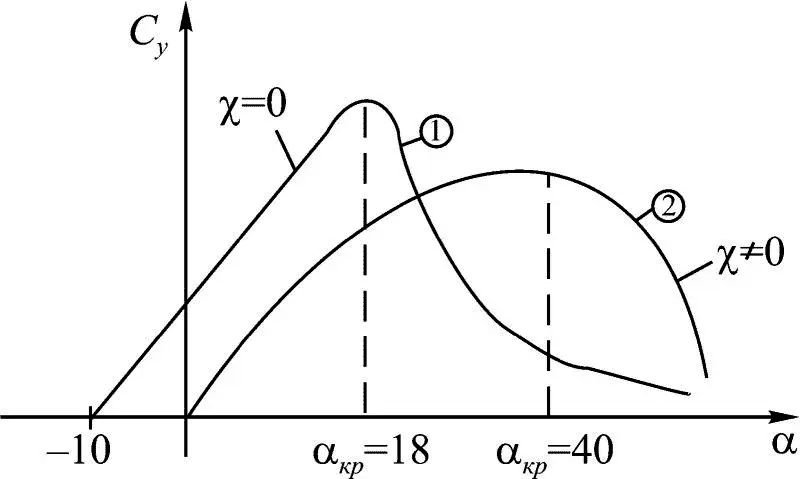
Рис. 1.17

Пусть возникла угловая скорость ω х относительно оси ОХ (продольной), что обусловливает изменение угла атаки α. Угол атаки, измеряемый флюгариком α ф , остается неизменным. Величина C у ( z ) получит приращение

Δ C у ( z ) = Δ C у (Δα( z ,ω x )).

Пусть ω x увеличивается. При этом увеличивается C у ( z ), и при достижении C укр в сечении z угол атаки достигает критического значения α кр . При этом α ф остается неизменным, что обусловливает необходимость введения зависимости α кр = α кр (α ф ,ω х ). Если мы будем рассматривать C у ( z ,α), где α – угол атаки в сечении z по размаху крыла, когда ω x ≠ 0, β = 0, то получим:

C у ( z ,α) = C у (α ф ) + Δ C у ( z ,ω х ,β).

При этом

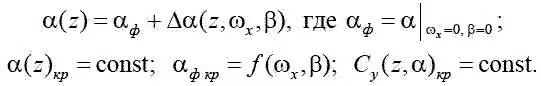
Изменение критического угла атаки самолета при полете с ω x ≠ 0 приведено на рис. 1.18. При этом зависимость C у (α) преобразуется в C у (α,ω х ), и тогда α кр = α кр (ω х ) ; C у кр = C у кр (α,ω х ), когда .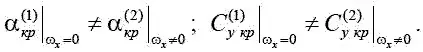

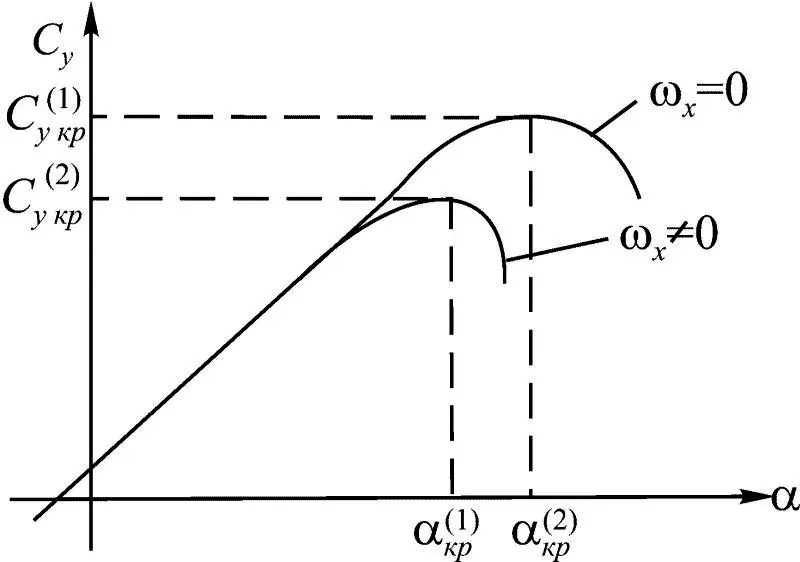
Рис. 1.18

Эти различия обусловлены методами измерения угла атаки, т. е. методами съема информации. При этом на рис. 1.18 представлены зависимости C у от угла атаки α ф , измеренного флюгариком в невозмущенном потоке воздуха.

Пусть самолет совершает полет при α < α кр и ω x = 0. Угол атаки α измеряется флюгариком α ф в невозмущенном потоке воздуха α нв = α ф. Рассмотрим сечение крыла на расстоянии z от оси симметрии. В рассматриваемой ситуации С у = С у ( z ) = С у (α( z )).

Если мы хотим строить алгоритм вычисления 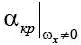, то должны воспользоваться зависимостью:

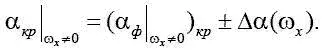
Таким образом, α кр , измеренное флюгерным датчиком, – это некоторая функция ω х , а в общем случае и β; в то же время критический местный угол в сечении z крыла и соответственно С укр не изменяются.

Рассмотрим особенности α кр измеренного флюгариком, т. е. α ф . В стационарном плоском режиме полета достаточно гарантировать α ф ≤ α кр , чтобы обеспечить безопасность ЛА. В случае, когда рассматривается стационарное пространственное движение при β ≠ 0, необходимо при ограничении α ф учитывать α кр = α кр (β). В случае, когда имеет место переход от дозвуковых к сверхзвуковым режимам полета при β ≠ 0, необходимо учитывать М, и тогда α кр = α кр (β, M ).

В случае, когда имеет место ω х , тогда α кр = α кр (β, M ,ω x ). При пространственном маневре α кр = α кр (β, M , 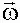). Таким образом, предлагается в качестве координаты контроля и ограничения использовать не α ф , а C у ( z ) сечения крыла. Информация о C у ( z ) – фундаментальная характеристика области Ω доп особенно в динамическом режиме, когда необходимо отслеживать C у maxили C у кр. В этом режиме измерить α( z ) флюгариком невозможно, так как флюгарик неадекватно отображает значение α( z ).

Влияние угла скольжения β на величину критического угла атаки представлено на рис. 1.19.

Изменение поля сил аэродинамического давления, обусловленное β ≠ 0, связано с изменением местного угла атаки α( z ,β), когда .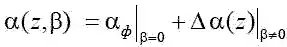

При этом критический угол атаки, измеренный флюгариком, не зависит от β так же, как и ранее от ω х . Влияние числа Маха на величину C у кр = C у св , где C у св – подъемная сила сваливания, представлена в виде графика на рис. 1.20.

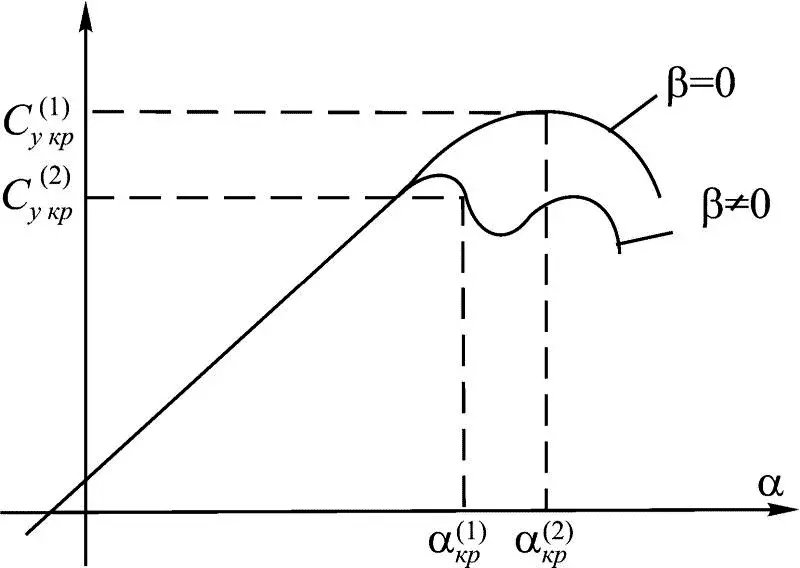
Рис. 1.19