Владимир Живетин - Системы аэромеханического контроля критических состояний

Особенности контроля состояния аэродинамических систем. Три разные динамические системы:

1) маневренный самолет (истребитель);

2) гражданский неманевренный самолет;

3) вертолет,

требуют различного подхода при их исследовании.

Контроль состояния таких динамических систем, соответствующие управления должны строиться таким образом, чтобы обеспечить максимально возможную эффективность и безопасность полетов. Современные системы контроля и управления обеспечивают безопасное состояние самолета как материальной точки по большой совокупности параметров и их оптимальное выдерживание. Однако на сегодня остались нерешенными ряд проблем контроля и управления, обеспечивающих безопасность и оптимальность полетов самолета как системы с распределенными параметрами, представляющие собой поле аэродинамического давления (ПАД) на несущих поверхностях. Именно ПАД реагирует на отклонения органов управления 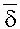= (δ рв ,δ э ,δ рн ), где δ рв , δ э , δ рн – угол отклонения руля высоты, элеронов, руля направления, реализуя пространственные маневры стационарной и нестационарной динамики.

Нестандартное, нерасчетное состояние ПАД как в стационарном, так и в нестационарном режиме его изменений создает опасное состояние самолета. Переход в квазихаотическое состояние ПАД делает самолет неуправляемым, возникает режим самовращения, когда, например, элероны не отклонены [6].

В качестве примера физической сути ограничений на параметры для динамических режимов рассмотрим устойчивость самолета.

Сегодня положено начало общей теории движения самолета относительно центра масс при маневрах с большими диапазонами изменения параметров движения. При исследовании нестационарных процессов определяющая роль безопасности полета принадлежит нахождению связи между величинами углов отклонения органов управления самолетов (δ э ,δ pв ,δ pн ) и теми изменениями параметров его движения – углов атаки (α) и скольжения (β) и проекций вектора угловой скорости 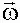= (ω x ,ω у ,ω z ), которые обусловливают эти отклонения.

При анализе пространственных движений, сопровождающихся отклонением органов управления с большой скоростью, исследуется взаимосвязное изменение всех параметров движения. Более того, величины предельных установившихся значений углов атаки и скольжения и проекций вектора угловой скорости 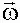= (ω x ,ω у ,ω z ) являются неоднозначными функциями отклонений органов управления. Математически это означает, что для каждой комбинации компонент вектора управлений 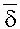= (δ рв ,δ рв ,δ э ), создающих соответствующие компоненты вектора 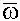, имеется несколько особых точек решений управлений движения, характеризующих взаимоотношение поля сил аэродинамических давлений и инерционных сил и моментов. При этом построение области допустимых (безопасных) и критических (опасных) значений (α, β, 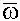) представляется проблематичным.

Каждой комбинации отклонения (δ рв ,δ рн ,δ э ) соответствует определенная система особых точек в фазовом пространстве параметров движения (α, β, 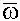), а значения этих параметров (α 0, β 0, 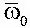) в момент времени, предшествующий отклонению рулей, являются начальными. При исследовании пространственного движения современных самолетов, когда 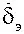велика, необходимо оценить: максимальные значения α, β, n y , достигаемые при этом; возможность режима инерционального вращения (потерю управляемости элеронами). Потеря управляемости элеронами связана с движением самолета с угловой скоростью крена 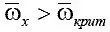при неотклоненных элеронах.

Движение самолета имеет наиболее сложные характеристики при значениях угловых скоростей крена, близких к критическим скоростям, когда инерционные и аэродинамические моменты близки по величине. Для маневренных самолетов эта область играет важную роль при определении областей Ω доп и Ω кр .

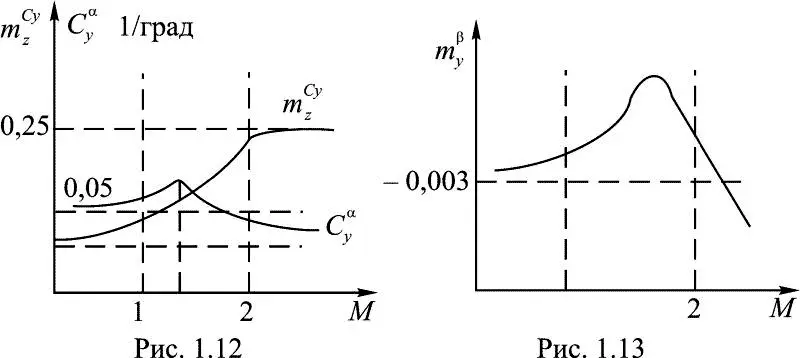
Рассмотрим роль поля сил аэродинамического давления при пространственном маневре. Для маневренных самолетов запас продольной устойчивости при переходе с дозвуковых скоростей на сверхзвуковые существенно возрастает в связи со сдвигом по потоку фокуса крыла, когда возрастает производная m z Cy (рис. 1.12). При этом запас путевой устойчивости самолета m β y уменьшается при возрастании М (рис. 1.13).

На дозвуковых скоростях полета меньшей по величине критической скоростью крена является ω z – критическая скорость тангажа, а при M > 1 меньшей критической скоростью крена становится величина ω(β) – критическая скорость, определяемая движением рысканья. Таким образом, значения критических скоростей имеют тенденцию к уменьшению, что увеличивает вероятность их достижения.

Отметим важную особенность. Если угловая скорость крена в процессе движения приближается либо превосходит меньшую из критических скоростей крена, то устойчивость движения самолета уменьшается либо теряется. При этом α и β начнут монотонно возрастать, и если вращение не будет прекращено, то самолет может войти на недопустимо большие α и β, и при больших скоростных напорах, когда Y > Y дon , наступит разрушение конструкции самолета.

Отметим особенности состояния самолета в двух ситуациях следующими многомерными управлениями: (δ э , δ рв ), (δ э , δ рн ).

I. Предельно-допустимые (критические) параметры движения при многомерном управлении (δ э ,δ рв ) и прежде всего при маневре крена.

Величины предельных установившихся значений углов атаки а, скольжения β и проекций вектора угловой скорости (ω x ,ω у ,ω z ) являются неоднозначными функциями отклонений органов управления, т. е. имеется несколько особых точек системы уравнений движения. Во всех случаях линейный характер зависимости угловой скорости крена ω x от отклонения элеронов δ э нарушается.

В этом состоит принципиальное отличие результатов, полученных согласно теории линейных дифференциальных уравнений.