Владимир Живетин - Системы аэромеханического контроля критических состояний
- Название:Системы аэромеханического контроля критических состояний
- Автор:
- Жанр:
- Издательство:Институт проблем риска, ООО Информационно-издательский центр «Бон Анца»
- Год:2010
- Город:Москва
- ISBN:978-5-98664-060-0, 978-5-903140-40-4
- Рейтинг:
- Избранное:Добавить в избранное
-
Отзывы:
-
Ваша оценка:
Владимир Живетин - Системы аэромеханического контроля критических состояний краткое содержание
Монография предназначена для специалистов в области контроля и управления самолетом.
Системы аэромеханического контроля критических состояний - читать онлайн бесплатно ознакомительный отрывок
Интервал:
Закладка:
В динамическом режиме полета поле аэродинамического давления порождает аэродинамические силы, которые характеризуются энергетическим потенциалом не только на поверхности, но и на некотором удалении от поверхности, создавая неконтролируемое влияние на приемники информации. В связи с этим в динамическом режиме возникают непреодолимые трудности устранения методических ошибок. Существенным моментом при этом является имеющая место зависимость коэффициента подъемной силы:
C у = C у (α, β, M, W x , W у, W z, δ рв , δ рн , δ э , t ),
и соответственно опасные состояния самолета, которые характеризуются многофункциональными областями:
Ω кр = Ω кр ( C y, m z, m x, m y ),
где m x, m z, m y – моменты относительно осей X, Y, Z соответственно; W x , W y , W z – горизонтальная, вертикальная, боковая по оси ОZ составляющие потока воздуха в месте установки датчиков системы контроля.
Особенности ПСАД при пространственном движении
При несимметричном полете, например полете со скольжением, или наличии достаточно больших возмущений ПСАД приобретает сложную форму (отличную от горизонтального полета), которая зависит от параметров траектории полета. При этом возникают перекрестные связи в образовании ПСАД, что обусловливает зависимость момента крена и момента рыскания от угла атаки. Аналогично для подъемной силы Y = R y и продольного момента М z необходимо учитывать влияние скольжения.
Как правило, при анализе возмущенного движения самолета пользуются приближенными линейными аппроксимациями вида [6]:
– для коэффициента момента крена
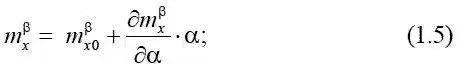
– для коэффициента продольного момента
m z = m α z ·α + C 1β;
– для коэффициента подъемной силы
C y = C α y ·α + C 2β,
где С 1 , С 2 – постоянные величины;
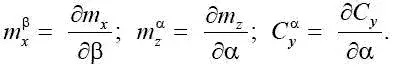
Сказанное указывает на наличие аэродинамического взаимодействия бокового и продольных движений. Такое взаимодействие в некоторых режимах полета существенно, и тогда линейная аппроксимация (1.5) обладает недопустимыми погрешностями контроля, создавая опасные состояния (режимы полета).
В случае, когда необходимо решать такие задачи, как:
– анализ безопасности полета на посадке (взлете) при резкой смене ветра со встречного на попутный;
– анализ статистической нагрузки при оценке ресурса;
– анализ безопасности реализации пространственного динамического режима полета;
– анализ безопасности полета в области скоростей вблизи скорости флаттера,
необходимо уравнение движения центра масс и относительного центра масс
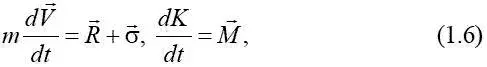
где 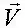 – вектор скорости движения ЛА в инерциальной (земной) системе координат OX д , OY д , OZ д ;
– вектор скорости движения ЛА в инерциальной (земной) системе координат OX д , OY д , OZ д ; 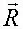 – вектор аэродинамических внешних сил;
– вектор аэродинамических внешних сил; 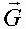 – вектор сил тяжести;
– вектор сил тяжести; 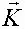 – вектор момента количества движения;
– вектор момента количества движения; 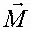 – вектор аэродинамического момента внешних сил относительно центра масс, дополнить в общем случае уравнениями, описывающими изменения ПСАД во времени и пространстве, вида
– вектор аэродинамического момента внешних сил относительно центра масс, дополнить в общем случае уравнениями, описывающими изменения ПСАД во времени и пространстве, вида
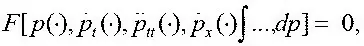
где р (·), 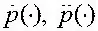 – соответственно давление, скорость и ускорение его изменения по времени в произвольной точке на поверхности самолета;
– соответственно давление, скорость и ускорение его изменения по времени в произвольной точке на поверхности самолета; 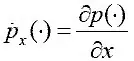 – производная по пространственной координате x .
– производная по пространственной координате x .
Отметим, что правые части (1.6) включают параметры ПСАД, характеризующие движение самолета относительно воздуха (воздушная скорость 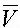 , угол атаки α). Левые части уравнений (1.6), учитывающие инерционные силы и моменты, зависят, например, от скорости движения относительно Земли, т. е. путевой скорости полета. В общем случае они не равны. Приравнивая их, мы допускаем ошибки в системах контроля, формируя их и выдерживая параметры траектории в области допустимых состояний.
, угол атаки α). Левые части уравнений (1.6), учитывающие инерционные силы и моменты, зависят, например, от скорости движения относительно Земли, т. е. путевой скорости полета. В общем случае они не равны. Приравнивая их, мы допускаем ошибки в системах контроля, формируя их и выдерживая параметры траектории в области допустимых состояний.
Рассмотрим модель ПСАД в случае, когда перепад давления р j (·) рассматривается в n точках на поверхности крыла. При этом будем полагать p j ( · ) = p j ( t,x;C α), где x = ( x 1 ,…,x N ), а искомые распределенные функции р 1( t,x;C α), р 2( t,x;C α) … рассматриваются как решения системы из n уравнений, определенных в пространстве R N , с координатами x = ( x 1 ,x 2 ,…,x N ) вида
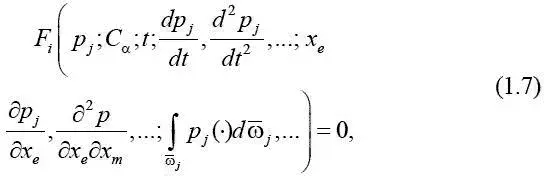
где C α – параметрическая функция конструкции, реализующая управления.
Переменные р j включают пространственные х с и временные t координаты, в том числе ω x , ω у , ω у , α, β, M и т. д.
Решения p j описывают состояние поля сил аэродинамических давлений, поэтому их можно называть переменными состояния. Предполагается, что F i зависят от k параметров C α, включающих отклонения органов управления самолетом δ рв , δ рн, δ э, δ з , δ пр – соответственно руля высоты, руля направления, элеронов, закрылков, предкрылков, в том числе числа Рейнольдса и т. п. Эти параметры называются управляющими.
Область интегрирования 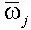 по пространственным координатам задается исходя из дополнительных соображений. Проблема анализа (решения) системы (1.10) чрезвычайно сложна, и, как правило, при этом используются различные предположения. Одним из таких путей является выделение следующих режимов полета:
по пространственным координатам задается исходя из дополнительных соображений. Проблема анализа (решения) системы (1.10) чрезвычайно сложна, и, как правило, при этом используются различные предположения. Одним из таких путей является выделение следующих режимов полета:
1) стационарный: p ≠ 0; 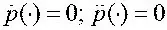 ;
;
2) квазистационарный: р ( · ) ≠ 0; 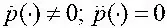 ;
;
Интервал:
Закладка:










