Владимир Живетин - Управление рисками рыночных систем (математическое моделирование)

Гипотеза В α.Фактическое значение индикатора рыночной системы x ф находится вне области допустимых состояний, т. е. имеет месть событие B α. С помощью средств контроля или оценки имеем А γ, В γили С γ.

Гипотеза С α.Фактическое значение индикатора системы x ф находится вне области допустимых состояний, т. е. имеет место событие С α. С помощью средств контроля или оценки имеем А γ, В γили С γ.

В итоге имеем различные события S ij , которые сгруппируем следующим образом:

I. ( А α∩ А γ) ;→S 11;

II. ( А α∩ С γ); ( А α∩ В γ); → S 21, S 22;

III. ( С α∩ А γ); ( В α∩ А γ); → S 31, S 32;

IV. ( С α∩ С γ); ( В α∩ В γ); → S 41, S 42;

V. ( С α∩ В γ);. ( В α∩ С γ); → S 51, S 52.

Полученные события характеризуют следующие контролируемые состояния экономической системы:

I. Безопасные (в норме).

II. Опасное ложное из-за ошибок измерения (фактическое безопасное).

III. Опасное нам неизвестное (пропуск со стороны системы контроля).

IV. Опасное известное (форс-мажор).

V. Опасное известное – нонсенс (несообразность), т. е. S 51, S 52практически невозможны.

Каждое из событий S ij характеризуется соответствующей вероятностью:

1) вероятность Р 11= Р ( S 11) = Р ( А α∩ А γ) – когда поступает информация о допустимом состоянии х , и фактическое его значение х ф допустимо;

2) вероятности Р 21= Р ( S 21) = Р ( А α∩ С γ) и Р 22= Р ( S 22) = Р ( А α∩ В γ) – когда значение х ф находится в допустимой области, а система контроля фиксирует недопустимое значение;

3) вероятности Р 31= Р ( S 31) = Р ( С α∩ А γ) и Р 32= Р ( S 32) = Р ( В α∩ А γ) – значение х ф находится вне допустимой области, но система контроля создает сигнал о допустимом состоянии объекта;

4) вероятности Р 41= Р ( S 41) = Р ( С α∩ С γ) и Р 42= Р ( S 42) = Р ( В α∩ В γ) – значение х ф находится вне области допустимых состояний, одновременно система контроля подтверждает это состояние;

5) вероятности Р 51= Р ( S 51) = Р (С α∩ В γ) и Р 52= Р ( S 52) = Р ( В α∩ С γ) – значение х ф находится вне области допустимых состояний, например по минимуму (максимуму), и система контроля показывает, что рыночная система находится в недопустимой области, но с противоположной стороны, т. е. превысила максимальное (минимальное) значение.

Совокупность S ij ( 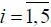; j = 1,2) образует полную группу несовместных событий, т. е. .

Событие ( А α∩ А γ) соответствует правильному анализу состояния системы, а вероятность Р 11характеризует безопасное ее состояние, при котором осуществляется основная цель рыночной системы. Если же осуществляется такой контроль и управление, при которых наступают события S 21, S 22, S 31, S 32, S 41, S 42, S 51, S 52, то цель, поставленная перед управляющей системой, не выполняется, так как возникают неоправданные (лишние) расходы по управлению. Эти состояния характеризуются потерями и называются опасными.

В качестве основных интегральных характеристик невыполнения цели, т. е. макрорыночного риска, будем рассматривать вероятности событий ( S 21, S 22), ( S 31, S 32), ( S 41, S 42), ( S 51, S 52):

Р 2= Р ( S 21 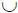S 22) = Р 21( S 21) + Р 22( S 22),

Р 3= Р ( S 31 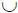S 32) = Р 31( S 31) + Р 32( S 32),

Р 4= Р ( S 41 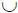S 42) = Р 41( S 41) + Р 42( S 42),

Р 5= Р ( S 51 S 52) = Р 51( S 51) + Р 52( S 52).

В дальнейшем из рассмотрения можно исключить ситуации, когда система контроля нам указывает на критическую ситуацию, но мы не имеем в своем распоряжении управления, способного возвратить в область безопасных состояний.

Система контроля, для которой события S 51или S 52теоретически осуществимы, порождает случайные величины или процессы, когда х ф находится в области ( х ф < 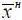), а измеренное значение х изм – в области ( х и зм > 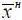) (рис. 1.30), или наоборот.

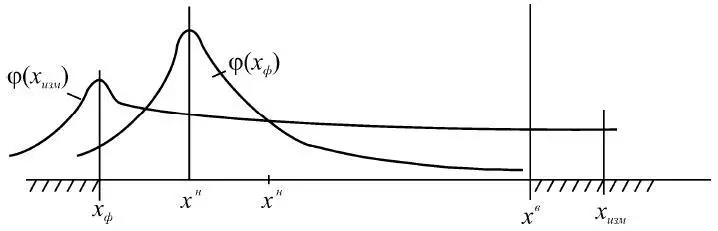
Рис. 1.30

Если учитывать физическую нереализуемость такого контроля, то события S 51и S 52невозможны, в силу того, что их вероятность пренебрежимо мала.

На примере вероятностей Р 2, Р 3, которые наиболее важны при оценке рыночного риска макроэкономики, рассмотрим построение математической модели, позволяющей получить численную оценку вероятностей Р 2и Р 3. Для вероятностей Р 1, Р 4, Р 5все выводы аналогичны.

В качестве основных интегральных характеристик невыполнения цели будем рассматривать величины вероятностей событий ( А α∩ В γ), ( В α∩ А γ), а также ( А α∩ С γ), ( С α∩ А j ):

P ( S 21) + P ( S 22) = P ( A α∩ C γ) + P ( A α∩ B γ);

P ( S 31 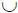S 32) = P ( S 31) + P ( S 32) = P ( A γ ∩ C α) + P ( B α ∩ A γ).

Вероятность Р 2характеризует появление ложной информации, поэтому назовем ее вероятностью ложной оценки состояния, а Р ( В' γ | А α) = Р ′ 2 – условной вероятностью ложной оценки состояния, где В' γ= ( В 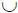γ С γ).

Вероятность Р 3характеризует такое состояние, при котором превышение х значения х кр не фиксируется в процессе контроля или оценки параметра х. Эту вероятность назовем вероятностью опасной ситуации, а Р ( В' α | А γ) = Р' 3 – условной вероятностью опасной ситуации , где В' α= В α 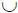C α. Вероятности Р 2и Р 3отличаются от Р′ 2, Р' 3на Р ( А α) и Р ( А γ), которые не зависят от характеристик средств оценки или контроля и поэтому при анализе и синтезе системы контроля могут не рассматриваться. Однако это отличие необходимо учитывать при назначении допустимых значений Р 2, Р 3, Р′ 2, Р' 3. При этом Р 2и Р 3отличаются от Р' 2, Р' 3на постоянные множители.