Бенуа Мандельброт - Фрактальная геометрия природы

В первом приближении (играющем центральную роль в главе 7) я предположил, что реки и водоразделы образуют сопряженные заполняющие плоскость древовидные фигуры. Вообще говоря, такое описание можно применить только к картам; как только мы вводим высоту, замечательная симметрия между деревьями рек и водоразделов нарушается. В самом деле, если пренебречь озерами, то точки, принадлежащие дереву водораздела, всегда являются либо локальными максимумами (холмами), либо локальными седловыми точками (перевалами), тогда как точки дерева реки никогда не бывают ни локальными минимумами, ни седловыми точками. А поскольку в броуновских и дробных броуновских моделях локальные минимумы безусловно присутствуют, можно с полной уверенностью сказать, что деревьев рек в них нет, - и это еще один удар по моим броуновским моделям.

После того, как чаши заполнены, рек, как таковых, уже не остается – лишь ветвящиеся цепочки озер (бесконечно мелких), похожие на кактусы с дисковидными ветвями. Что касается водоразделов, то они образуют дерево; я полагаю, что это дерево представляет собой ветвящуюся кривую с размерностью D<2 , однако оно может оказаться и кривой с положительной площадью и, как следствие, размерностью D=2 . Возможны также и другие, самые различные, варианты, но их лучше приберечь до более подходящего случая.

Взглянем на высказанные ранее утверждения в более широкой перспективе, для чего рассмотрим сначала простой, одномерный случай – дробную броуновскую функцию B H (x) из прямой в прямую. Островом в таком рельефе будет интервал [x',x"] , в котором B H (x)>0 при x' , а B H (x')=B H (x'')=0 . Обозначим через x=x 0 точку, в которой значение функции B достигает максимума (вероятность существования нескольких максимумов x 0 исчезающее мала), и определим функцию B * H(x) следующим образом:

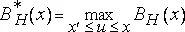, если x находится в интервале [x',x 0] ,

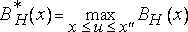, если x находится в интервале [x 0,x"] .

Очевидно, что необходимым и достаточным условием для того, чтобы капля, отправившись в путь из точки (x,z) , добралась до океана, двигаясь все время по невосходящей траектории, является справедливость неравенства z≥B * H(x) . Капли, для которых верно неравенство B H(x)* H(x) , остаются в чашах навсегда, а значение z=B * H(x) соответствует уровню воды, достигаемому после заполнения всех чаш. Эта наша функция B * представляет собой не что иное, как чертову лестницу Леви (см. рис. 399 и 400), идущую вверх от точки x' до точки x 0 и объединенную с другой лестницей, идущей вниз от x 0 до x'' .

Она непрерывна, но недифференцируема, и изменяется на множестве нулевой длины. Любая капля воды, добавленная вблизи высочайшей точки материка, вскоре вольется в океан, двигаясь только по плоским областям, чередующимся с «водопадами».

Капли, которые не могут утечь в океан, заполняют область B H(x)* H(x) . Эта область несвязна, так как она не содержит точек, в которых B * H=B H , а ее связные участки представлены расположенными на материке чашами. Длина чаши определяется как расстояние между двумя последовательными нулевыми значениями разности B * H−B H . Благодаря масштабной инвариантности функции распределение этой длины следует гиперболическому закону; известно, что при H=½ показатель распределения также равен ½ , и я убежден, что этот показатель всегда совпадает со значением параметра H . Отношение наибольшей длины чаши к |t'−t"| имеет наибольшее значение при H→0 и наименьшее при H→1 .

Вернемся к броуновскому материку B H (x,y) на плоской Земле. И в этом случае функция B * H(x,y) определяется с помощью аналогичного условия: капля воды, отправившись в путь из точки, расположенной на высоте z>B * H(x,y) , может добраться до океана по невосходящей траектории, любая точка которой находится выше материка. Как и ранее, пространственная область, внутри которой справедливо неравенство B H(x,y)* H(x,y) , распадается на отдельные связные открытые области, определяющие чаши.

Сравним эти чаши с чашами на очень тонком срезе материка, ограниченном параллельными стенами y=0 и y=ε , применяя введенные ранее обозначения B H (x) и B * H(x) . Согласно определению функции B * H(x) , пути утекания воды ограничиваются траекториями, которые находятся между упомянутыми стенами, тогда как определение B * H(x,0) допускает гораздо более широкий выбор возможных путей утекания. Следовательно, B * H(x,0)* H(x) почти при любом x . То есть функция B * H(x,0) , равно как и любое другое вертикальное сечение функции B * H(x,y) , представляется намного более интересной, нежели функция B * H(x) . Эти сечения представляют собой чертовски террасированные сингулярные функции с бесконечным количеством пикообразных локальных максимумов и плоских локальных минимумов. Если верно мое наиболее правдоподобное предположение, то последние покрывают почти все точки материка.

Так как сумма площадей чаш не может быть больше площади материка, чаши можно расположить в порядке убывания площади, а это означает, что множество чаш счетно. Следовательно, береговая линия материка B H , соответствующая некоторому случайному значению z 0 , почти наверняка не содержит двойных точек.

Значит, совокупную границу всех чаш можно получить следующим образом: возьмем некоторое счетное множество значений z m - сюда почти наверное не войдет значение, при котором береговая линия образует петлю. Цензурируем множество береговых линий посредством удаления из всех значений z 0 =z m тех, что соответствуют береговым линиям глухих долин. К полученному объединению цензурированных береговых линий добавим его предельные точки.

Для любого M>2 возможно непосредственное обобщение в броуновскую функцию от M - мерной переменной x={x 0 ,...x M } . Из приведенного выше рассуждения для случая M=2 можно видеть, что при заданной функции B H (x) разница между B * H и B H уменьшается по мере увеличения M . В пределе, когда M=∞ , а B H - есть броуновская функция в гильбертовом пространстве, из классических результатов, полученных Полем Леви, следует что B * H−B H≡0 . Останется ли это тождество истинным для всех M>M крит, где M крит <���∞ ?