Бенуа Мандельброт - Фрактальная геометрия природы

Рис. 372 и 373. Броуновские береговые линии и «гряды» островов

Первоначально эти иллюстрации были призваны подчеркнуть один только что обнаруженный важный эффект. Когда размерность D рельефа достигает значения 2,5 и превосходит его, океан начинает демонстрировать явную и усиливающую тенденцию к разделению на отдельные округлые «моря». Эти моря сообщаются друг с другом, но вместе с тем каждое сохраняет выраженную индивидуальность. Острова при этом выстраиваются в «гряды». Тот же эффект (хотя и не так явственно) наблюдается и в горных хребтах, присутствующих на всех «пейзажах» на рис. 370, 371 и 379.

Это отсутствие изотропии в выборках полностью согласуется с изотропией порождающего механизма.

Фигуры, изображенные на этих рисунках, эквивалентны (за исключением затравки) плоским сечениям хлопьев на рис. 25 и 26 (которые объясняются в конце главы 30). Здесь, как и на рис. 25 и 26, мы используем усеченную версию одного периода периодического варианта ожидаемого процесса. Это уменьшает зависимость общих очертаний от D . Общие очертания действительно броуновских береговых линий различаются сильнее, чем показано на наших иллюстрациях.

В главах 34 и 35 обсуждается эффект, связанный с упомянутыми грядами.

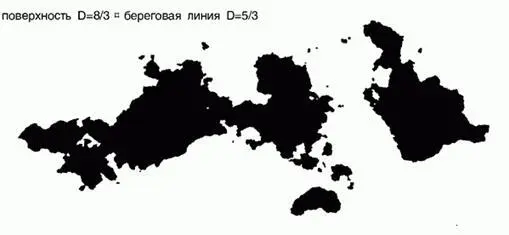
Рис. 374. Линии уровня в дробных броуновских ландшафтах

На каждом из рисунках этой страницы представлены по две – три линии уровня (береговые линии показаны жирными линиями) для дробных броуновских функций. При построении этих фигур использовались одинаковые программа и затравка, но различны размерности: D~1,3333 (верхняя фигура) и D~1,1667 (нижняя фигура). Тщательно рассмотрев оба рисунка , можно убедиться, что с географической точки зрения они выглядят вполне правдоподобно: верхний сойдет за побережье горного озера, нижний же соответствует более равнинной местности.

Эти кривые выглядят гораздо менее «изрезанными», чем кривые с той же размерностью D на рис. 373. Причина заключается в том, что на тех иллюстрациях каждое сечение демонстрирует ярко выраженный максимум; сколько-нибудь систематических уклонов там почти нет. Здесь же, напротив, перед нами склон огромной горы, который имеет выраженный общий уклон. Благодаря их «общему» виду, фигуры на этой странице можно рассматривать как увеличенные версии какого-нибудь особенно изрезанного малого участка береговой линии с рис. 373.

Сравнение этих различных линий уровня дает лучшее понимание того, насколько широки рамки допустимых взаимодействий между иррегулярностью и фрагментацией даже при фиксированном значении размерности D .

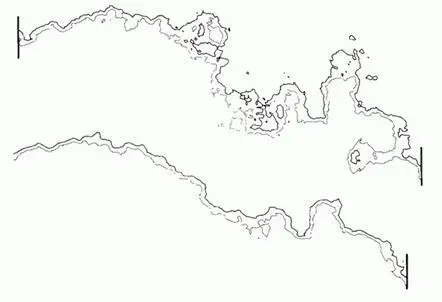
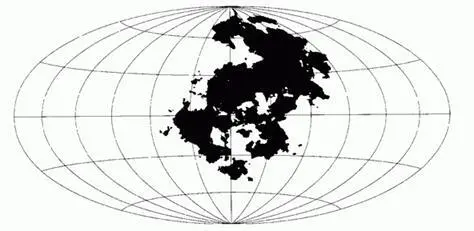
Рис. 375 и С11 (вверху). Броуновская Пангея (размерность береговой линии D=3/2 )

На поверхности «далекой планеты», изображенной на рис. С11 (вид из космоса), мы видим очертания воображаемой фрактальной Пангеи. Ее рельеф был получен посредством компьютерной реализации (насколько мне известно, это было проделано впервые) случайной поверхности, которой мы обязаны Полю Леви: броуновской функции из точек на сфере (широта и долгота) в скалярные величины (высота). Уровень моря был выбран таким образом, чтобы три четверти общей площади оказалось под водой. Береговую линию получили интерполяцией.

На этом рисунке та же Пангея изображена на хаммеровской карте – проекция, предпочитаемая приверженцами вегенеровской теории континентального дрейфа.

Насколько эта модельная Пангея похожа на «настоящую»? Мы вовсе не надеемся, что совпадут какие-то конкретные локальные детали; нас интересует лишь совпадение степеней извилистости – как локальной, так и глобальной. Как и следовало ожидать, до совершенного сходства наша модель не дотягивает. В самом деле, размерность D береговой линии модельной Пангеи составляет 3/2 , в то время как гипотетические рисунки в учебниках геологии приписывают реальной Пангее то же значение D , что наблюдается в очертаниях современных континентов, т.е. D~1,2 . Если вдруг появятся какие-то новые данные, совместимые с D=3/2 , то мы получим возможность объяснить геометрию Пангеи, основываясь на весьма элементарных тектонических допущениях.

Фракталы в неевклидовом пространстве.В неевклидовой геометрии Римана роль плоскости выполняет сфера. Неевклидовы геометрии, таким образом, неевклидовы только наполовину: они занимаются евклидовыми фигурами на неевклидовых носителях. Бóльшая часть настоящего эссе демонстрирует аналогичную «половинчатость»: мы изучаем неевклидовы фигуры в евклидовом пространстве. Представленная на рисунке Пангея объединяет наши подходы, поскольку представляет собой пример неевклидовой фигуры на неевклидовом же носителе.

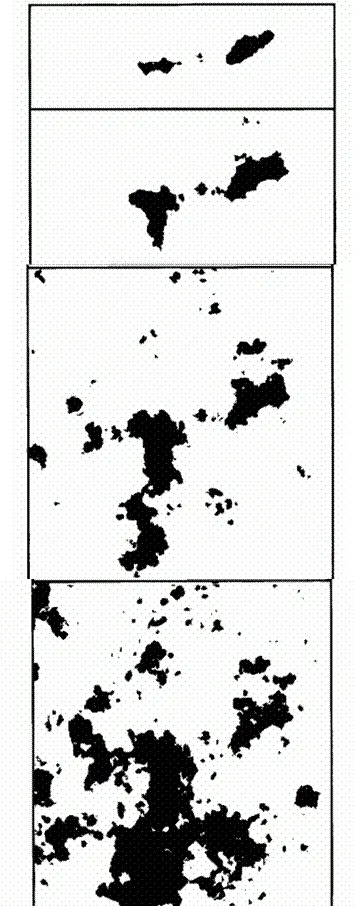
Рис. 377. Первые известные примеры броуновских береговых линий (обыкновенных и дробных)

Мое утверждение о том, что с помощью должным образом выбранных дробных броуновских функций можно достаточно правдоподобно моделировать земной рельеф, основывалось первоначально на вот этих четырех моделях береговых линий. Руководствуясь исключительно сентиментальными соображениями, я перенес их (вместе с рис. 375) сюда из французского эссе 1975 г. почти без изменений, разве что черные области закрашены теперь более аккуратно, благодаря чему оказалось возможным передать исходное построение более точно.

Когда значение D близко к единице (верхний рисунок), береговая линия слишком прямолинейна, чтобы выглядеть реалистичной.

А вот очертания берегов со второго сверху рисунка (D=1,3000) вполне могли бы занять достойное место на карте из настоящего атласа. Большой остров слева явно напоминает Африку или Южную Америку (в зеркальном отражении), а большой остров справа очень похож на Гренландию (если повернуть страницу на 90° против часовой стрелки). Наконец, если повернуть страницу на 90° по часовой стрелке, то из обоих островов вместе получаются слегка исхудавшая Новая Зеландия и сдвоенный остров Баунти.