Бенуа Мандельброт - Фрактальная геометрия природы

Леви (см. [306, 307, 308, 309, 410]) вводит понятие броуновских функций из пространства Ω в вещественную прямую, где Ω представляет собой либо обычное пространство ℝ E (расстояние |PP 0| определяется как отрезок прямой), либо сферу в пространстве ℝ E+1 (расстояние определяется вдоль геодезических линий), либо гильбертово пространство. Для каждой из соответствующих броуновских функций значений разности B(P)−B(P 0 ) является гауссовой случайной величиной с нулевым средним и дисперсией G(PP 0|) , где G(x)=x . Рекомендую также обратить внимание на статьи [421] и [70].

Представление броуновской функции в виде белого гауссова шума, когда Ω - сфера.В этом случае функция B(P) строится, как описано в главе 28: на поверхность сферы накладывается слой белого гауссова шума, а функция B(P) определяется как интеграл этого белого шума по поверхности полусферы, северный полюс которой совпадает с точкой P . Вообще-то, я предпочитаю несколько иной вариант, в котором берется половина интеграла по одной полусфере, а затем вычитается половина интеграла по другой полусфере. Такая процедура позволяет обобщить второй процесс, описанный в подразделе 4.

Представление броуновской функции в виде белого гауссова шума, когда Ω−ℝ E [79].Этот случай требует более сложного алгоритма (алгоритм был предложен Ченцовым). Наиболее наглядное представление об этом алгоритме можно получить, когда пространство Ω есть ℝ 2 , и B(0,0)=0 . Построим вспомогательный цилиндр единичного радиуса с координатами u и θ и наложим на него слой белого шума. Далее (в модифицированном мною [379] варианте алгоритма) проинтегрируем этот шум по прямоугольнику от θ до θ+dθ и от 0 до u . Получим броуновскую функцию из прямой в прямую, которая обращается в нуль при u=0 ; обозначим ее через B(u,θ,dθ) . Для каждой точки (x,y) плоскости броуновские составляющие B(x cos θ+y sin θ,θ,dθ) статистически независимы, а их интеграл по θ равен B(x,y) .

В работе Ганголли [161] (отдельные моменты которой были предвосхищены еще Ягломом [608]) функция B(P) обобщается до случая G(x)=x 2H (см. предыдущий подраздел). Здесь, однако, не приводится явного алгоритма для построения результирующей функции. Для того чтобы заполнить этот пробел, я обобщил в [379] построение Ченцова, заменив каждую функцию B(u,θ,dθ) двусторонне определенной дробной броуновской функцией из прямой в прямую.

О размерности D см. в [610, 611].

О моделировании с помощью БПФ см. [582].

Зададим дисперсию G(x) , отличную от G(x)=x , составим сумму 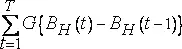и интерполируем ее линейно для нецелочисленных T . Результат (который мы обозначим через B G (t)−B G (0) ) асимптотически масштабно - инвариантен, если существует некоторая функция A(T) , такая, что предел 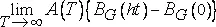невырожден при любом h∈(0,1) . Мюррей Розенблатт рассмотрел случай G(x)=x 2 −1 . В статье [551] показано, что эта задача тесно связана с эрмитовым рангом дисперсии G в ряд Эрмита. О более новых находках в этом направлении можно узнать из работ [554] и [110].

Дополнительные материалы по этой теме (а также по нецелочисленным основаниям систем счисления) можно найти в главе XII «Фракталов» 1977 г.

Связь гиперболического распределения с масштабной инвариантностью основывается на следующем свойстве (присущем только гиперболическому распределению): распределение нормированной усеченной случайной величины « U/u 0 , если U/u 0 >1 » не зависит от u 0 .

Доказательство.Пусть имеется некоторое основное распределение P(u) , причем нормированная усеченная с. в. W=U/u 0 имеет обычное условное распределение P(wu)/P(u 0) . Нам нужно, чтобы это условное распределение было одинаковым для u 0 =h' и u 0 =h'' . Запишем v'= ln h' и v''= ln h'' и рассмотрим функцию R= ln P(u) как функцию от v= ln h . Для получения искомого тождества P(uh')/P(h')=P(uh")/P(h") необходимо, чтобы при любом выборе значений v,v' и v'' выполнялось равенство R(v'+v)−R(v')=R(v"+v)−R(v") . А для этого функция R должна быть линейной функцией от v .

Музыка обладает, по меньшей мере, двумя достойными упоминания скейлинговыми свойствами.

Темперированные музыкальные гаммы и их связь с частотным спектром модифицированной функции Вейерштрасса.Из всех слов современного английского языка, восходящих к латинскому корню scala («лестница»), самым употребительным является, конечно же, не скейлинг, прочно обосновавшийся в нашем эссе, а слово scalу в значении «музыкальная гамма», под чем подразумевается некий дискретный спектр, получаемый умножением частот. В темперированной гамме значения частот располагаются в логарифмической последовательности. Например, додекафоническая (двенадцатитоновая) гамма соответствует основанию b=2 1/12 ; в результате бóльшая часть основных тонов любого музыкального инструмента приходится на относительно низкие частоты его полного частотного диапазона, высокие же частоты достаются немногим избранным.

Экстраполируя такой спектр в обе стороны на частоты, не воспринимаемые человеческим ухом, получим спектр, неотличимый от спектра функции Вейерштрасса (соответствующим образом модифицированной, см. с. 533) с тем же значением b . Следовательно, для того, чтобы добавить низких частот в музыкальное произведение, достаточно ввести в оркестр новые инструменты, способные производить низкие тоны желаемой частоты.

Согласно теореме Эйлера – Фурье, самая общая периодическая функция представляется в виде ряда линейно упорядоченных гармоник и, следовательно, последовательность основных тонов некоего эталонного музыкального произведения может быть представлена только очень суженными функциями.

Музыка как масштабно-инвариантный (1/f) шум (по Р.Ф. Фоссу).Второй скейлинговый аспект музыки связан с изменением во времени различных характеристик звукового сигнала: например, мощности (определяемой как квадрат интенсивности) или мгновенной частоты (определяемой как количество пересечений сигналом нулевого уровня за единицу времени). Фосс и Кларк [580, 581] (см. также [164]) отмечают, что в произведениях таких различных композиторов, как Бах, Бетховен и «Битлз», обе упомянутые характеристики звукового сигнала представляет собой масштабно-инвариантные шумы (или 1/f - шумы, см. с. 356).