Бенуа Мандельброт - Фрактальная геометрия природы

После k этапов каскада взвешенного створаживания количество вихрей, в которых оказывается сосредоточена бóльшая часть массы, составляет величину порядка b kD* (при общем количестве вихрей b 3k ), где

D *=−b(r 3W)>=3−bW> .

В частности, если величина W дискретна и ее возможные значения w i имеют относительные вероятности p i , имеем

D *=3−∑p iw ilog bw i .

Случай D * >0; D=D * .Мера, порождаемая взвешенным створаживанием аппроксимируемого фрактально однородной мерой с размерностью D=D * ,получаемой так же, как описано в главе 23.

Случай D * <0; D=0 .Количество непустых ячеек асимптотически стремится к нулю, а это значит, что предел почти наверное оказывается пустым.

В общей сложности, носитель массы аппроксимируется замкнутым множеством с размерностью D= max (0,D * ) .

Сечения.Аналогичным образом масса, заключенная в плоских и линейных сечениях, сосредотачивается в относительно малом количество вихрей: b D*−1 для плоских сечений (при общем числе вихрей b 2 ) и b D*−2 для линейных сечений (при общем числе вихрей b ). То есть сечения невырождены при D * >1 (и, соответственно, D * >2 ) и аппроксимируются фракталами с размерностями D * −1 и D * −2 . Таким образом, размерности сечений в этом случае подчиняются тем же правилам, что и в случае лакунарных фракталов.

Новые случайные величины, инвариантные при взвешенном сложении.Пусть X - это случайная величина, которая асимптотически задает вес, заключенный внутри вихря любого порядка k или внутри его сечения прямой или плоскостью (размерность сечения обозначим через Δ ). Я показал, что величины X удовлетворяют функциональным уравнениям

,

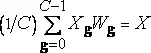где C=b Δ , величины W g и X g - независимые случайные величины, равенство же выражает идентичность распределения. Это уравнение представляет собой обобщение уравнения (L) , рассматриваемого в разделе устойчивые по леви случайные величины и функции. Решения этого уравнения являются обобщением устойчивых случайных величин и подробнее обсуждаются в цитированных выше статьях [378, 376] и [254].

В [367] описана вихревая решетка, сочетающая в себе абсолютное и взвешенное створаживание, позаимствованное у Кантора. Вихри не задаются заранее, но генерируются при построении с помощью того же статистического механизма, который используется для генерации заключенной в них массы. Кроме того, дискретные вихревые слои сливаются в такой решетке в непрерывный континуум.

Предельная логарифмически нормальная функция: обоснование.Произведем кое-какие последовательные модификации взвешенного створаживания на примере некоторой функции L(t) от одной переменной (выбранной из соображений простоты).

После n - го этапа плотность взвешенного створаживания задается функцией Y n (t) , такой, что приращение Δ ln Y n (t)= ln Y n+1 (t)− ln Y n (t) есть ступенчатая функция; изменяется эта функция только тогда, когда t представляет собой интеграл, кратный b −n =r n , в остальные же моменты времени ее значениями являются независимые случайные величины вида ln W . Положим теперь, что приращение Δ ln W является логарифмически нормальным со средним − ½( ln b) и дисперсией μ ln b . При этом ковариация между Δ ln Y n (t) и Δ ln Y n (t+τ) принимает на интервале |τ|n значение μ(lnb)(1−|τ|/r n) и обращается в нуль вне этого интервала. Функция Δ ln Y n (t) не может считаться гауссовой, поскольку совместное распределение ее значений при двух (или более) t не является многомерной гауссовой случайной величиной.

Первая модификация.Заменим все Δ ln Y n (t) соответствующими ΔlnY * n(t) , определяемыми как гауссовы случайные функции с практически той же ковариацией μ(lnb)exp(1−|τ|/r n) . В результате такой замены сохраняется «область зависимости» оригинала, однако нарушаются дискретные границы между вихрями продолжительности r n .

Вторая модификация.Заменим дискретный параметр n ln b непрерывным параметром λ . Сумма конечных разностей ΔlnY * n(t) заменяется при этом интегралом бесконечно малых дифференциалов d ln L λ (t) со средним − ½μdλ и дисперсией μdλ , а вихри становятся непрерывными.

Определение функции L(t) .Рассмотрим предел

.

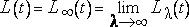Случайная величина ln L λ (t) является гауссовой со средним λ(t)>=−½λμ и дисперсией σ 2 L λ (t)=λμ . Отсюда λ(t)>=1 при всех λ . Однако предел функции L λ (t) может быть либо невырожденным, либо почти наверное равным нулю. Математического разрешения эта проблема пока не получила, однако можно, очевидно, придать строгий вид нижеследующим эвристическим рассуждениям. Они проводятся на примере более интересных функций L(x) от трехмерной переменной.

Множество концентрации предельной логарифмически нормальной меры.Удобным средством для получения представления о множестве, в котором значение L λ (x) не только не малó, но чрезвычайно велико, являются опорные квадраты со стороной r n . Это не искусственно навязанные субвихри, а всего лишь способ измерения. При n≫1 и фиксированном x вероятность того, что значение логарифмически нормальной функции L n lnb(x) окажется очень близко к нулю, чрезвычайно высока, т.е. на бóльшей части области определения значения этой функции чрезвычайно малы.

Поскольку функция L n lnb(x) непрерывна, изменение ее значения внутри ячейки со стороной r n очень невелико, а это значит, что к настоящей модели применим способ получения множества концентрации в случае взвешенного створаживания с логарифмически нормальной величиной W . Если пренебречь логарифмическими членами, то количество ячеек, составляющих бóльшую часть интеграла функции L n lnb(x) , имеет математическое ожидание Q=(r n) D* , где D * =3−μ/2 .