Бенуа Мандельброт - Фрактальная геометрия природы

.

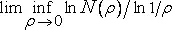Дальнейшее развитие этот подход получил в работе Колмогорова и Тихомирова [278], авторы которой, почерпнув вдохновение в шенноновской теории информации, окрестили величину lnN(ρ) ρ - энтропией множества S . Хокс [204] называет соответствующую размерность нижней энтропийной размерностью, а ее вариант, получаемый заменой liminf на limsup - верхней энтропийной размерностью. Кроме того, Хокс показывает, что размерность Хаусдорфа – Безиковича не может превышать нижней энтропийной размерности; они часто совпадают, но не всегда.

В [278] рассматривается также величина M(ρ) , определяемая как наибольшее количество точек в S , отстоящих друг от друга на расстояние, превышающее 2ρ . Для множеств, расположенных на прямой, M(ρ)=N(ρ) . Для других множеств величину

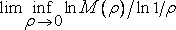
можно считать еще одной размерностью.

У Колмогорова и Тихомирова [278] величина ln M(ρ) называется емкостью, что в высшей степени неудачно ввиду того, что в теории потенциала уже существует такой термин с совершенно иным и, на мой взгляд, более оправданным значением. В особенности следует избегать искушения определить выведенную в предыдущем абзаце размерность, как емкостную размерность. См. раздел потенциалы и емкости, 3.

Из главы 8 нам известно, что в том случае, когда пространство Ω представляет собой интервал [0,1] или вещественную прямую, пыль S полностью определяется своим дополнением, т.е. объединением максимальных открытых интервалов или пустот (в некоторых построениях все пустоты являются тремами).

Троичная канторова пыль C на интервале [0,1].Длины пустот составляют в сумме единицу и следуют гиперболическому распределению P(U>u)=Fu −D . Следовательно, порядок длины λ n n - й пустоты (в порядке уменьшения размера) равен n −1/D .

Обобщенные линейные множества нулевой меры Лебега.Поведение длины λ n при n→∞ рассмотрено в работе Безиковича и Телора [29]. Существует некоторый вещественный показатель D BT , такой, что ряд ∑λ n d сходится при d>D BT (в частности, сходится к 1 при d=1 ). Таким образом, D BT представляет собой инфимум вещественных чисел d , при которых ∑λ n d<���∞ . Можно показать, что D BT ≥D . Хокс (см. [204], с. 707) доказывает, что величина D BT совпадает с верхней энтропийной размерностью, причем иногда легче поддается оценке.

Предостережение.Если S не является множеством нулевой меры, показатель D BT не является размерностью. Этот показатель сродни показателю, описанному в главе 15, и показателю Δ из главы 17.

Показатель аполлониевой упаковки.У показателя D BT имеется аналог в случае аполлониевой упаковки (см. главу 18). Он был введен в 1966 г. З. А. Мельзаком, а Бойд [51] показывает, что этот показатель представляет собой (как и предполагалось) размерность Хаусдорфа – Безиковича остаточного множества.

В некоторых открытых множествах (т.е. не содержащих свои предельные точки) можно наблюдать серьезное несоответствие размерностей.

Множество концевых точек трем канторовой пыли самоподобно и характеризуется теми же значениями N и r , что и вся канторова пыль, т.е. его размерность подобия совпадает с размерностью подобия канторовой пыли. Однако оно является счетным, а это означает, что его размерность Хаусдорфа – Безиковича равна нулю. Если добавить сюда предельные точки пыли, то мы получим саму канторову пыль, и несоответствие исчезнет «в пользу» размерности подобия, которая для этого множества является более важной характеристикой.

Еще один простой пример, который я называю множеством Безиковича, рассматривается в разделе нелакунарные фракталы, 3.

Пусть μ(x) - некоторая неубывающая функция от x ∈[0,1]. Если максимальные открытые интервалы, в которых значение μ постоянно, составляют в сумме дополнение замкнутого множества S , то мы говорим, что множество S является опорным для dμ(x) . Преобразование Фурье – Стилтьеса функции μ имеет вид

.

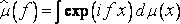Самые гладкие функции μ дают наивысшую возможную скорость уменьшения 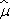. Обозначим через D F наибольшее вещественное число, при котором, по меньшей мере, одна функция μ(x) с носителем S удовлетворяет равенству

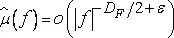при f→∞ для всех ε>0 ,

но ни одна μ(x) не удовлетворяет

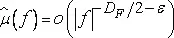при f→∞ для некоторых ε>0 .

Выражение « a=O(b) при f→∞ » означает здесь, что 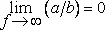. Когда множество S заполняет весь интервал [0,1], величина D F бесконечна. И напротив, когда S - одна – единственная точка, D F =0 . Интересно, что, когда S представляет собой множество нулевой меры Лебега, величина D F конечна и не превышает размерности Хаусдорфа – Безиковича D этого множества. Неравенство D F ≤D показывает, что фрактальные и гармонические свойства фрактального множества связаны между собой, но не обязательно совпадают.

Для доказательства того, что эти размерности могут различаться, предположим, что S - это множество на прямой, причем его размерность D равна D F . Если рассматривать S как множество на плоскости, то размерность D не изменится, а D F обратится в нуль.

Определение.В качестве удобного способа обобщения некоторых гармонических свойств S , предлагаю назвать величину D F размерностью Фурье множества S .

Множества Сейлема.Равенство D F =D описывает целую категорию множеств, называемых множествами единственности, или множествами Сейлема (см. [255, 248]).