Бенуа Мандельброт - Фрактальная геометрия природы

Эмпирическое правило и эвристика.Интересующие нас в прецедентных исследованиях фракталы оказываются, как правило, множествами Сейлема. Поскольку величина D F во многих случаях легко определяется из экспериментальных данных, можно использовать ее для оценки D .

Неслучайные множества Сейлема.Неслучайная канторова пыль является множеством Сейлема только тогда, когда коэффициент r удовлетворяет определенным теоретико-числовым свойствам.

Случайные множества Сейлема.Случайная канторова пыль является множеством Сейлема тогда, когда ее случайность достаточно велика для нарушения любой арифметической закономерности.

Оригинальный пример, предложенный самим Р. Сейлемом, очень сложен. В качестве альтернативного примера можно привести пыль Леви: в [253] показано, что спектр dL(x) (здесь L(x) - лестница Леви, см. рис. 399) в среднем почти совпадает со спектром дробной броуновской функции из прямой в прямую и представляет собой сглаженный вариант спектра функции Гаусса – Вейерштрасса.

В монографии [248] (теоремы 1, с. 165, и 5, с. 173) показано, что образ компактного множества S с размерностью δ относительно дробной броуновской функции из прямой в прямую с показателем H представляет собой множество Сейлема с размерностью D= min (1,δ/H) .

Канторова пыль не является множеством Сейлема.Троичная канторова пыль появилась в свое время на свет в результате поисков Георгом Кантором множества единственности (см. [616], I, с. 196), - поисков, которые не увенчались успехом. (Кантор тогда забросил гармонический анализ и – за неимением лучшего – создал теорию множеств.) Обозначим канторову лестницу через C(x) . Спектр dC(x) имеет ту же общую форму, что и спектр dL(x) , однако содержит, в отличие от последнего, некоторое количество случайно расположенных острых пиков неубывающего размера, из чего можно заключить, что D F =0 . См. [216].

Для теории множеств единственности наличие этих пиков играет решающую роль, однако на практике они вовсе не столь значимы. В большинстве случаев при оценке спектральной плотности пики игнорируются, и в расчет принимается только общая форма спектра, определяемая размерностью D .

Материалы по этой теме (связанной с кривыми Пеано) можно найти в главе XII «Фракталов» 1977 г.

До недавних пор в прикладной статистике принимались как само собой разумеющиеся два следующих допущения в отношении временных рядов: предполагалось, что 2><���∞ и что случайная величина X обладает краткосрочной зависимостью. Я, однако, показал (см. главу 37), что эмпирические последовательности данных с длинными хвостами часто лучше интерпретируются в свете допущения 2>=∞ . С вопросом же о том, является та или иная последовательность данных слабо (краткосрочно) или сильно (долгосрочно) зависимой, мы впервые столкнулись еще тогда, когда я ввел долгосрочную зависимость для интерпретации феномена Херста (см. главу 27).

Такая смесь длинных хвостов и очень долгосрочной зависимости могла бы завести статистиков в тупик, поскольку стандартные методы второго порядка, рассчитанные на неизменную зависимость (корреляцию, спектры), руководствуются допущением 2><���∞ . Есть. Однако, альтернатива.

Можно пренебречь распределением величины X(t) и проанализировать ее долгосрочную зависимость с помощью нормированного размаха; иначе такая процедура называется R/S - анализом. Этот статистический метод, предложенный в [408] и получивший математическое обоснование в [384], основан на различии между краткосрочной и очень долгосрочной зависимостями. В этом методе вводится постоянная J , которая называется коэффициентом Херста, или R/S - показателем, и может принимать любые значения в интервале от 0 до 1.

Значимость постоянной J можно описать еще до ее определения. Особое значение J=½ характерно для независимых, марковских и других случайных функций с краткосрочной зависимостью. Таким образом, для того, чтобы узнать, присутствует ли в эмпирических данных или в выборочных функциях очень долгосрочная непериодическая статистическая зависимость, достаточно проверить, приемлемо ли статистически предположение J=½ . Если нет, то такая зависимость присутствует, а мера ее интенсивности определяется разностью J−½ , значение которой можно оценить на основании имеющихся данных.

Главное достоинство такого подхода заключается в том, что показатель J устойчив по отношению к маргинальному распределению. То есть он эффективен не только в тех случаях, когда последовательности данных или случайные функции являются почти гауссовыми, но и тогда, когда распределение X(t) настолько далеко от гауссова, что 2(t)> расходится, а в этом случае не работает ни один из методов второго порядка.

Определение статистического R/S - размаха. В непрерывном времени t определим X *(t)= 0∫ tX(u)du , X 2*(t)= 0∫ tX 2(u)du и X *2=(X *) 2 . В дискретном времени i определим X * (0)=0 и 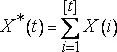; здесь [t] - целая часть t . Для всякого d>0 (величину d назовем запаздыванием) определим скорректированный размах суммы X * (t) на временнóм промежутке от 0 до d в виде

.

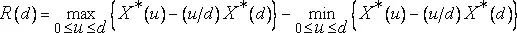Оценим далее выборочное среднеквадратическое отклонение величины X(t) :

S 2(d)=X 2*(d)/d−X *2/d 2 .

Величина Q(d)=R(d)/S(d) называется статистическим R/S - размахом или самонормированным самокорректированным размахом суммы X * (t) .

Определение R/S - показателя J .Предположим, что существует некоторое вещественное число J , такое, что при d→∞ величина (1/d J)[R(d)/S(d)] сходится по распределению к некоторой невырожденной предельной случайной величине. Как доказано в [384], из этого предположения следует, что 0≤J≤1 . В этом случае говорят, что функция X имеет R/S - показатель J и постоянный R/S - префактор.

Сделаем более общее предположение: пусть к некоторой невырожденной предельной случайной величине сходится по распределению отношение [1/d JL(d)][R(d)/S(d)] , где L(d) - некоторая медленно изменяющаяся на бесконечности функция, т.е. функция, удовлетворяющая условию L(td)/L(d)→1 при d→∞ для всех t>0 . Простейшим примером такой функции является L(d)= ln d . В этом случае говорят, что функция X имеет R/S - показатель J и R/S - префактор L(d) .