Бенуа Мандельброт - Фрактальная геометрия природы

Если μ>6 (т.е. D * <0 ), то Q→0 при λ→∞ , и функция L(x) почти наверное вырождена.

Если 4<���μ<6 (т.е. 0 * <1 ), то функция L(x) имеет размерность D=D * и невырождена, однако ее следы на плоскостях и прямых почти наверное вырождены.

Если 2<���μ<4 (т.е. 1 * <2 ), то функция L(x) и ее следы на плоскостях невырождены (размерности D * и D * −1 , соответственно), однако ее следы на прямых почти наверное вырождены.

Если 0<���μ<2 (т.е. 2 * <3 ), то и функция L(x) , и ее следы на плоскостях и прямых невырождены (размерности D * , D * −1 и D * −2 , соответственно).

Исследование относительной перемежаемости может привести нас и к другим определениям размерности. Вместо множества в метрическом пространстве рассмотрим некую меру μ(S) , которая определена в ограниченном подпространстве Ω (в соответствующем σ - поле, включающем в себя и шары) и обладает нижеперечисленными свойствами. (А) Когда S - шар, μ(S)>0 , а μ(Ω)=1 , т.е. «множество, в котором μ>0 » совпадает с пространством Ω . (Б) Руководствуясь интуитивными соображениями, можно однако предположить, что мера μ «концентрируется» внутри очень малой части пространства Ω . Необходимы новые способы количественного выражения (Б) .

При заданных ρ>0 и 0<���λ<1 рассмотрим множества ∑ λ , для которых верно неравенство μ(Ω−∑ λ)<���λ . Обозначим через N(ρ,∑ λ) инфимум количества шаров радиуса ρ , необходимых для покрытия множества ∑ λ . Определим

N(ρ,λ)=infN(ρ,∑ λ) .

За некоторыми, на мой взгляд, многообещающими эвристическими оценками скрываются выражения «размерностного» вида

;

;

,

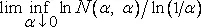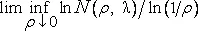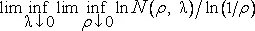строгое исследование которых можно было бы только приветствовать. Разумеется, эвристические оценки заменяют значение infN(σ,λ) действительным N(σ,∑ λ) относительно некоторого приемлемого покрытия ∑ λ .

Размерность Хаусдорфа – Безиковича D играет центральную роль в современной теории классических и обобщенных потенциалов (потенциалов Марселя Рисса) с ядрами вида |u| −F , где F≠E−2 . Из появившихся в недавнее время неэлементарных исследований теории потенциалов рекомендую обратить внимание на книги Дюплесси ([122], глава 3) и Ландкофа [287] (в последней материал изложен более подробно).

Мы вскоре сможем убедиться в том, что особое значение D=1 тесно связано с ньютоновским потенциалом в ℝ 3 . Эта связь лежит в основе замечаний, высказанных в главе 9 относительно различных космологических теорий, согласно которым D=1 , - таких, например, как теории Фурнье и Джинса – Хойла.

Я полагаю, должна существовать возможность переформулировать эти теории в виде следствий из ньютонова закона всемирного тяготения.

Следовательно, должна существовать и возможность вывести отклонение наблюдаемого значения D~1,23 от единицы из неньютоновских (релятивистских) эффектов.

Как уже упоминалось в главе 9, Бентли и Ньютону было известно о том, что в теории гравитационного потенциала имеет место эффект, аналогичный кеплерову эффекту пылающего неба («парадоксу Ольберса»). Предположим, что E=3 , что масса M(R) , заключенная внутри сферы радиуса R с центром в точке ω , пропорциональна R D , где D=3 , и что ядро потенциала является ньютоновским и имеет вид R −F , где F=1 . Масса, заключенная внутри оболочки толщины dR и радиуса R , пропорциональна R D−1 ; следовательно, полный потенциал в точке ω , определяемый как ∝∫R −FR D−1dR=∫RdR , расходится в бесконечности. Расхождения в бесконечности не будет, если D=3 , а F>3 , т.е. если потенциал не является ньютоновским. Тот же результат мы получим и в модели Фурнье – Шарлье с F=1 и D<1 .

Для общего интеграла ∫R D−1−FdR условие сходимости в бесконечности очевидно: D . Таким образом, устанавливается однозначная связь между D и F ; значению F=1 , в частности, соответствует D=1 .

Эту связь исследовали Д. Пойа и Д. Серё, в окончательном же виде ее сформулировал О. Фростман в [158]. Главное усовершенствование заключается в том, что рассуждение теперь распространяется не только на точку начала координат ω , но на все точки, принадлежащие множеству S (компактному). Рассмотрим единичную массу, распределенную на множестве S так, что область du содержит массу dμ(u) . В точке t ядро |u| −F дает потенциальную функцию

∏(t)=∫|u−t| −Fdμ(u) .

Для измерения «протяженности» множеств де Ла Вале Пуссен применил физическую концепцию электростатической емкости. Идея такова, что если емкость C(S) множества S достаточно высока, то масса, которую мы можем «перетасовать» для достижения наименее возможного максимального потенциала, равна μ .

Определение.Найдем супремум потенциала по всем точкам t , затем – инфимум полученного результата относительно всех возможных распределений единичной массы на множестве S и, наконец, положим

.

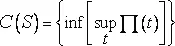Если используется ядро 1/r , то такой минимальный потенциал и в самом деле создается электрическими зарядами на проводящем множестве.

Эквивалентное определение.Величина [C(S)] −1 представляет собой инфимум (среди всех распределений массы, носителем которой является множество S ) энергии, определяемой двойным интегралом

∫∫|t−u| −Fdμ(s)dμ(t) .

Между величинами C(S) и F имеет место простое соотношение. Когда показатель F , используемый при определении емкости C(S) , больше, чем размерность D Хаусдорфа – Безиковича, C(S) обращается в нуль, - это означает, что даже при «наиболее эффективном» распределении массы по множеству S потенциал в какой-то из точек бесконечен. Когда же F меньше D , емкость множества S положительна. То есть размерность Хаусдорфа – Безиковича выступает здесь, согласно Пойа и Серё, как емкостная размерность. Тождественность этих понятий была в наиболее общем виде доказана Фростманом [158].