Бенуа Мандельброт - Фрактальная геометрия природы

Я, в свою очередь, обнаружил, что вследствие исключения из рассмотрения значений B>1 определение стационарности оказывается недостаточно общим для многих прецедентных исследований.

Условно стационарные спорадические процессы.Например, теория фрактальных шумов (см. главу 9) позволяет предположить, что процесс, состоящий из броуновских нулей стационарен в ослабленной форме. В самом деле, предположим, что где-то в промежутке между t=0 и t=T имеется хотя бы один нуль. Результатом такого предположения будет случайный процесс, зависящий от T как от дополнительного внешнего параметра. Я отмечал, что совместное распределение значений X(τ+t m ) не зависит от t при условии, что все моменты времени τ+t m находятся между 0 и T . Таким образом, нестационарный процесс броуновских нулей неявно включает в себя целый класс случайных процессов, каждый из которых условно стационарен, чего часто бывает вполне достаточно.

Процессы этого класса так тесно взаимосвязаны, что в [352] я даже предложил рассматривать их как один обобщенный стохастический процесс, называемый спорадическим процессом. Отличие такого процесса от стандартного случайного процесса заключается в том, что мера μ(Ω) всего выборочного пространства Ω бесконечна. То есть эту меру никак нельзя нормализовать к виду μ(Ω)=1 . О бесконечной мере μ(Ω) для случайных переменных писал еще Реньи [489]. Для того чтобы мера μ(Ω)=∞ не привела к катастрофе, в теории обобщенных случайных величин делается допущение о том, что эти величины наблюдаются только будучи обусловленными некоторым событием C , таким, что 0<���μ(C)<���∞ .

Хотя применимость случайных переменных Реньи очень ограниченна, спорадические функции оказываются иногда весьма полезными: в частности, с их помощью мне в [352] удалось избежать в нескольких случаях инфракрасной катастрофы, объяснив тем самым существование некоторых масштабно-инвариантных шумов с B∈[1,2] .

Эргодичность. Перемешивание.Различным интерпретациям подвергается также и понятие эргодичности. В математической литературе понятие эргодичности включает в себя различные формы перемешивания. Существуют процессы с сильным перемешиванием и процессы со слабым перемешиванием. Различие между этими формами (если судить о нем по математическим трудам) может показаться весьма незначительным и далеким от реальных природных феноменов. Не позволяйте ввести себя в заблуждение – это не так. Например, масштабно-инвариантные шумы с 0 представляют собой процессы со слабым перемешиванием и ни в коем случае не с сильным.

Четвертое недоразумение (относительно возможности предельной сходимости к B(t) ).Широко распространено мнение, согласно которому высказывание «процесс X(t) стационарен» равносильно утверждению о том, что его текущую сумму 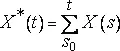можно нормализовать таким образом, чтобы она сходилась к броуновскому движению. Математикам давно известно, что это мнение лишено каких бы то ни было оснований (см. [177]), а во многих из прецедентных исследований настоящего эссе участвуют функции X(t) , которые ему прямо противоречат благодаря либо эффекту Ноя (2(t)>=∞) , либо эффекту Иосифа (бесконечная зависимость, как в f −B - шумах с B>0 ). Следует сказать, однако, что почти все мои прецедентные исследования были на некотором этапе a priori раскритикованы неким «экспертом», который утверждал, что исследуемые феномены явно нестационарны, и, следовательно, мои стационарные модели изначально обречены на неудачу. Рассуждение ошибочное, но психологически очень значимое.

Заключение.Вокруг границы между математически стационарными и нестационарными процессами не прекращаются бурные семантические диспуты. На практике же граница оккупирована процессами, которые хотя и не отвечают нашим интуитивным представлениям о стационарных процессах, все же способны выступать в роли объектов научного исследования. Эти процессы весьма пригодились и мне – как в настоящем эссе, так и в остальной исследовательской работе.

Лексические проблемы.И снова возникает необходимость в новых терминах. Возьму на себя смелость порекомендовать термин установившийся в качестве а) синонима того, что математики называют «стационарный и такой, что сумма X * (t) сходится к B(t) », и б) термина для обозначения того интуитивного понятия, которое исследователи-практики склонны именовать «стационарностью». Обратное понятие можно обозначить терминами неустановившийся или блуждающий.

В одной из своих ранних работ (а именно: в [373]) я предложил называть установившиеся процессы лапласовыми и мягкими. Последнее слово употреблено в значении «безопасный, легко контролируемый»; это значение показалось мне вполне подходящим, поскольку, имея дело с таким случайным процессом, можно не опасаться каких-либо сюрпризов с его стороны – не стоит ждать от него тех резких отклонений и разнообразных конфигураций, благодаря которым анализ блуждающих случайных процессов представляет собой более сложное, но и гораздо более интересное занятие.

Среди достоинств гиперболического распределения отметим непревзойденную формальную простоту и инвариантность при усечении (см. раздел масштабная инвариантность при усечении). Другие преобразования, оставляющие его инвариантным, нас сейчас не интересуют. Гораздо большее значение для нас имеют сейчас распределения, инвариантные при сложении. Гиперболическими они являются лишь асимптотически, а Поль Леви выбрал для них в свое время в качестве названия донельзя перегруженный термин: «устойчивые распределения». Он же ввел и понятие устойчивого процесса, в котором участвуют как гиперболическое, так и устойчивое распределения.

До публикации моих работ устойчивые случайные величины считались явлениями «патологическими» и даже «чудовищными»; единственное исключение составлял случайный вектор Хольтсмарка, о котором мы поговорим в подразделе 9. Я предложил некоторые области приложения устойчивых случайных величин, важнейшие из которых описаны в главах 31, 32 и 37; Кроме того, ниже (подраздел 4) упоминается о возможности применения таких величин в генетике.

Литература.Существует огромное количество различных источников, но ни один из них нельзя счесть удовлетворительным. В монографии Феллера ([148], том II) материал по устойчивости представлен, пожалуй, в самом полном объеме, однако он разбросан по всей книге, и порой очень трудно отыскать необходимые сведения. Книга Ламперти [284] может послужить неплохим введением в курс дела. Рекомендую также и работу Гнеденко и Колмогорова [172], несмотря на ее почтенный возраст. Много полезных подробностей можно найти у Лукача [320]. Оригинальные трактаты Леви [302, 304] вряд ли придутся по вкусу всем, поскольку эти великие научные труды являют собой яркие образцы авторского стиля (см. главу 40).