Бенуа Мандельброт - Фрактальная геометрия природы

Если не считать трех исключений ( D=2 с β=0 , D=1 с β=0 и D=1/2 с β=1 ), нам не известны устойчивые по Леви распределения в замкнутой аналитической форме, однако свойства этих простых исключений можно обобщить и на другие случаи.

Во всех крайних асимметричных случаях с 0 плотность при x<0 обращается в нуль.

В результате обобщения того факта, что гауссова плотность равна exp(−1/2x 2 ) , мы имеем небольшой хвост крайних асимметричных случаев с 1 . Плотность здесь ∝exp(−c|x| D/(D−1)) .

При x→∞ плотность Коши ∝π −1x −D−1 , а плотность возвращений броуновской функции ∝(2π) −½x −D−1 . В общем виде, при любом D≠2 плотность в длинном хвосте (или хвостах) ∝x −D−1 .

В иных случаях поведение плотности ρ(u) приходится находить численно. В [335] приведены графики для крайнего асимметричного случая, в [336] к ним добавлены примечания относительно очень близких к 2 значений D , а в [341] – графики для симметричного случая. Методы быстрого преобразования Фурье значительно облегчают эту задачу, см. [120, 121].

Пусть X 1 и X 2 независимые случайные величины с одинаковой плотностью вероятности p(u) . Плотность вероятности величины X=X 1 +X 2 имеет вид

p 2(u)= −∞∫ ∞p(y)p(u−y)dy .

Если известно значение суммы u , то плотность условного распределения каждого из слагаемых y равна p(y)p(u−y)/p 2 (y) . Рассмотрим подробно форму этой плотности

Примеры.Когда плотность p(u) является гауссовой плотностью с единичной дисперсией, т.е. унимодальной функцией (или функцией с одним максимумом), условное распределение также является гауссовым с центром в точке ½u , а его дисперсия равна ½ , т.е. не зависит от u (см. раздел броуновские фрактальные множества, 3). При u→∞ относительные значения слагаемых почти равны.

Когда плотность p(u) представляет собой приведенную плотность Коши, т.е. снова унимодальную функцию, следует различать два очень непохожих случая. При |u|≤2 , что составляет половину всех значений u , условное распределение также унимодально, а наиболее вероятным значением снова является ½u . В противоположном случае (при |u|>2 ) значение ½u становится наименее вероятным (локально). При |u|=2 условное распределение разветвляется на две отдельные «огивы», центры которых расположены в окрестности точек y=0 и y=u . По мере того, как u→±∞ , становится все труднее отличить эти огивы от огив Коши с центрами в точках 0 и u .

Когда плотность p(u) представляет собой плотность возвращений броуновской функции, ситуация напоминает случай Коши, только еще более крайний, причем плотность условного распределения является бимодальной с вероятностью >½ .

Вывод: рассмотрим три последовательных возвращения в нуль некоторого случайного блуждания: T k−1 , T k и T k+1 . Если значение разности T k−1 −T k+1 велико, то точка среднего возвращения с наибольшей вероятностью располагается чрезвычайно близко либо к точке T k−1 , либо к T k+1 , вероятность же того, что она окажется где-нибудь посередине между крайними возвращениями, можно полагать наименьшей. Этот результат сродни одному знаменитому «противоестественному» правилу из теории вероятности: закону арксинуса Леви.

Рассмотрим теперь условное распределение величины U , если известно, что сумма M величин U g принимает очень большое значение u . В случае гауссова распределения результат, скорее всего, окажется таким: каждое слагаемое U g будет приблизительно равно u/M . В случае же Коши (равно как и в случае броуновских возвращений) следует ожидать прямо противоположного результата: все слагаемые, кроме одного, будут очень малы.

Несоответствие, заключенное в идее «одинаковых» вкладов в сумму.Из того, что слагаемые a priori одинаковы (т.е. имеют одинаковое распределение), следует, что их значения могут a posteriori оказаться либо почти равными (как в случае гауссова распределения), либо в различной степени неравными (как в случае устойчивого по Леви распределения при очень большом значении суммы).

Дана бесконечная последовательность X n , составленная из независимых и одинаково распределенных случайных величин. Центральная предельная задача формулируется следующим образом: возможно ли выбрать такие веса a n и b n , чтобы сумма 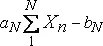имела нетривиальный предел при N→∞ ?

В стандартном случае n 2><���∞ ответ на этот вопрос будет стандартен и утвердителен: a N =1/√N , b N~n>√N , а предел является гауссовым.

Нестандартный случай n 2>=∞ намного сложнее: а) выбор a N и b N не всегда возможен; б) когда выбор возможен, предел оказывается устойчивым негауссовым; в) для того, чтобы показатель предела был равен D , достаточно, чтобы последовательность X n имела асимптотически гиперболическое распределение с показателем D (см. главу 38); г) необходимое и достаточное условие приводится в источниках, перечисленных в начале этого раздела.

Эти функции представляет собой случайные функции со стационарными независимыми приращениями, причем величина приращений X(t)−X(0) является устойчивой по Леви случайной величиной. Масштабный коэффициент a(t) , благодаря которому величина [X(t)−X(0)]a(t) остается независимой от t , должен иметь вид a(t)=t −1/D .

Этот процесс является обобщением обыкновенного броуновского движения на случай D≠2 .

Наиболее поразительное свойство функции X(t) заключается в том, что она разрывна и содержит скачки.

Случай D<1 .В этом случае X(t) не содержит ничего, кроме скачков, причем количество скачков, происходящих за интервал от t до t+Δt и имеющих абсолютное значение, превышающее u , представляет собой распределенную по закону Пуассона случайную величину с математическим ожиданием |Δt|u −D .