Бенуа Мандельброт - Фрактальная геометрия природы

Энергетический спектр функции W 0 (t) .Под энергетическим спектром понимается множество допустимых значений частоты f вместе со значениями энергии (квадратами амплитуд) соответствующих составляющих. На каждое значение частоты вида f=b n в функции W 0 (t) имеется спектральная линия энергии вида (1−w 2) −1w 2n . Следовательно, суммарное значение энергии на частотах f≥b n сходится и пропорционально w 2n =b −2nH =f −2H .

Сравнение с дробным броуновским движением.Суммарная энергия пропорциональна f −2H еще в нескольких рассмотренных нами ранее случаях: а) дробные периодические случайные функции Фурье – Броуна – Винера, допустимые частоты для которых имеют вид f=n , а соответствующие коэффициенты Фурье равны n H−½ ; б) случайные процессы с непрерывной спектральной плотностью совокупности, пропорциональной 2Hf −2H−1 . Последние процессы суть не что иное, как дробные броуновские функции B H (t) , описанные в главе 27. Например, при H=½ можно обнаружить кумулятивный спектр функции Вейерштрасса (f −1 ) в обыкновенном броуновском движении, спектральная плотность которого пропорциональна f −2 . Существенное различие: броуновский спектр абсолютно непрерывен, тогда как спектры функций Фурье – Броуна - Винера и Вейерштрасса дискретны.

Недифференцируемость.Для доказательства отсутствия у функции W 0 (t) конечной производной при любом значении t Вейерштрассу пришлось объединить два следующих условия: а) b - нечетное целое число, вследствие чего функция W 0 (t) представляет собой ряд Фурье, и б) log b (1+3π/2) . Необходимые и достаточные условия ( b>1 и 1 ) взяты нами из статьи Харди [194] .

Расходимость энергии.Привычному к спектрам физику условия Харди представляются очевидными. Применяя эмпирическое правило, гласящее, что производная функции вычисляется умножением ее k - го коэффициента Фурье на k , физик находит для формальной производной функции W 0 (t) , что квадрат амплитуды коэффициента Фурье с k=b n равен (1−w 2) −1w 2nb 2n . Так как совокупная энергия на частотах, больших b n , бесконечна, физику становится ясно, что производную W' 0(t) определить невозможно.

Интересно отметить, что Риман в поисках примера недифференцируемости пришел к функции 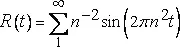, энергия спектра которой на частотах, бóльших f=n 2 , пропорциональна n −3 =f −2H , где H=¾ . Таким образом, применяя то же эвристическое рассуждение, можно предположить, что производная R'(t) недифференцируема. Заключение это верно лишь отчасти, поскольку при определенных значениях t производная R'(t) все-таки существует (см. [169, 528]).

Ультрафиолетовая расходимость / катастрофа.Термин «катастрофа» появился в физике в первом десятилетии ХХ века, когда Рэлей и Джинс независимо друг от друга разработали теорию излучения абсолютно черного тела, согласно которой энергия частотного диапазона ширины df в окрестности частоты f пропорциональна f −4 . Это означает, что совокупная энергия спектра на высоких частотах бесконечна – что оказывается весьма катастрофичным для теории. Поскольку источником неприятностей являются частоты, лежащие за ультрафиолетовой частью спектра, явление получило название ультрафиолетовой (УФ) катастрофы.

Всем известно, что Планк построил свою квантовую теорию на руинах, в которые обратила теорию излучения именно УФ – катастрофа.

Историческое отступление.Отметим (хотя я не совсем понимаю, почему никто не сделал этого раньше; во всяком случае, в доступных мне источниках я ничего похожего не обнаружил), что причиной смерти как старой физики (✝1900) , так и старой математики (✝1875) является одна и та же расходимость, подорвавшая их веру в то, что непрерывные функции просто обязаны быть дифференцируемыми. Физики отреагировали простым изменением правил игры, математикам же пришлось научиться жить с недифференцируемыми функциями и их формальными производными. (Последние представляет собой единственный часто применяемый в физике пример обобщенной функции Шварца.)

В поисках масштабно-инвариантного дискретного спектра. Инфракрасная расходимость.Хотя частотный спектр броуновской функции непрерывен, масштабно-инвариантен и существует при f=0 , частотный спектр функции Вейерштрасса, соответствующий тому же значению H , дискретен и ограничен снизу значением f=1 . Наличие нижней границы обусловлено исключительно тем обстоятельством, что число b у Вейерштрасса изначально было целым, а функция – периодической. Для устранения этого обстоятельства следует, очевидно, позволить n принимать любое значение от −∞ до +∞ . А для того, чтобы энергетический спектр стал масштабно-инвариантным, достаточно сопоставить каждой частотной компоненте b n амплитуду w n .

К сожалению, получаемый в результате ряд расходится, и повинны в этом низкочастотные компоненты. Такой дефект называется инфракрасной (ИК) расходимостью (или «катастрофой»). Как бы то ни было, с этой расходимостью приходится мириться, поскольку иначе нижняя граница f=1 вступает в противоречие с самоподобием, присущим энергетическому спектру f −2H .

Модифицированная функция Вейерштрасса, самоаффинная относительно фокального времени t=0 .Самая простая процедура, позволяющая продолжить частотный спектр f −2H функции Вейерштрасса до значения f=0 и избежать при этом катастрофических последствий, состоит из двух этапов: сначала получаем выражение W 0 (0)−W 0 (t) , и лишь затем позволяем n принимать любое значение от −∞ до +∞ . Добавочные члены, соответствующие значениям n<0 , при 0 сходятся, а их сумма непрерывна и дифференцируема. Модифицированная таким образом функция

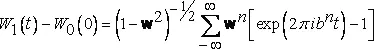
по-прежнему является непрерывной, но нигде не дифференцируемой.

Вдобавок, она масштабно - инвариантна в том смысле, что