Бенуа Мандельброт - Фрактальная геометрия природы

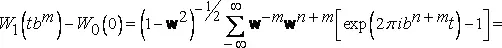
=w −m[W 1(t)−W 0(0)] .

Таким образом, функция =w −m[W 1(b mt)−W 0(0)] не зависит от m . Можно сказать иначе: при r=b m функция r −H[W 1(rt)−W 0(0)] не зависит от h . То есть функция W 1 (r)−W 0 (0) , ее вещественная и мнимая части самоаффинны относительно значений r вида b −m и фокального времени t=0 .

Гауссовы случайные функции с обобщенным спектром Вейерштрасса.Следующим шагом на пути к реализму и широкой применимости является рандомизация обобщенной функции Вейерштрасса. Простейший и наиболее естественный метод заключается в умножении ее коэффициентов Фурье на независимые комплексные гауссовы случайные величины с нулевым математическим ожиданием и единичной дисперсией. Вещественная и мнимая части получаемой в результате функции могут с полным правом называться функциями Вейерштрасса – Гаусса (модифицированными). В некоторых смыслах эти функции можно считать приближенными дробными броуновскими функциями. Когда значения H совпадают, их спектры настолько похожи, насколько позволяет то обстоятельство, что один из этих спектров непрерывен, а другой дискретен. Более того, к функциям Вейерштрасса – Гаусса применимы результаты Орея [457] и Маркуса [412] (см. с. 490), а фрактальные размерности их множеств уровня совпадают с фрактальными размерностями множеств уровня дробных броуновских функций.

Фрактальные свойства.Согласно теореме, доказанной в работах [317] и [30] (см. раздел эвристика липшица – Гёльдера), фрактальная размерность графика функции с некоторым показателем H , удовлетворяющей при всех x условию Липшица, находится в интервале от 1 до 2−H . Известно, что в случае броуновской функции с тем же кумулятивным спектром f −2H размерность принимает наибольшее возможное значений 2−H=D . Я предполагаю, что то же верно и для кривой Вейерштрасса. А размерность ее нуль – множества равна 1−H .

Нуль - множества родственных функций.Функции Радемахера представляет собой «ступенчатые» варианты синусоид вида sin(2πb nt) , где b=2 . Когда синус положителен (отрицателен, обращается в нуль), значение функции Радемахера равно 1 (соответственно, − 1 и 0 ) (см. [616], I, с. 202). Естественным обобщением функции Вейерштрасса является ряд, n - й член которого представляет собой произведение w n на n - ю функцию Радемахера. Эта обобщенная функция разрывна, однако ее спектральный показатель по-прежнему равен 2H . Учитывая прецедент в лице дробного броуновского движения, можно предположить, что размерность нуль – множеств функции Вейерштрасса – Радемахера окажется равной 1−H . Это предположение находит подтверждение в [31], однако только для целочисленных 1/H .

Сингх [526] упоминает о многих других вариантах функции Вейерштрасса. Размерность D нуль – множеств некоторых из них легко поддается оценке. Вообще, эта тема явно заслуживает более подробного исследования с учетом достижений современной теоретической мысли.

Классическое определение характеристической функции J(t) при заданном множестве S имеет следующий вид: J(x)=1 , если x∈S , и J(x)=0 , если x∉S . Когда множество S представляет собой канторово множество (салфетку или ковер) Серпинского, фрактальную сеть или любое множество из нескольких других классов фракталов, функция J(x) не совсем удобна. На мой взгляд, часто бывает удобнее заменить функцию J(x) другой функцией C(x) , которую ввел я и которую предлагаю назвать кохаристической.

Функция C(x) представляет собой случайно взвешенное среднее характеристических функций пустот множества S . Иными словами, в каждом отдельном пустом промежутке C(x) постоянна, а ее значения в других пустотах являются независимыми случайными величинами с одинаковым распределением.

Под старым и часто неверным названием ядерной функции функция C(x) вводится и исследуется в работах [347, 352, 357].

В качестве удобных источников общих сведений по теме рекомендую [231], [35], [497], [3].

Кантору приходила в голову мысль о том, что «при исследовании размерностей непрерывных множеств невозможно обойтись без общего понятия объема или величины», однако он, по всей видимости, не уделил ей должного внимания. Лебег полагает, что, имей Кантор полное представление о сложности стоящей перед ним задачи, ему вряд ли удалось бы достичь сколько-нибудь значительных результатов. Эта мысль получила дальнейшее развитие в работе Каратеодори [67] и была впоследствии воплощена Хаусдорфом [203].

Классическая процедура оценки площади плоской фигуры начинается с аппроксимации множества S с помощью набора очень маленьких квадратов; далее сторона каждого квадрата возводится в степень D=2 и полученные результаты складываются. Каратеодори [67] расширяет рамки этого традиционного подхода. Заменив квадраты дисками, он избегает зависимости от координатных осей; кроме того, с самого начала предполагается, что мы не знаем, является ли множество S стандартной евклидовой фигурой известной размерности, вложенной в известное пространство R E .

Заметим теперь, что если плоскую фигуру, вложенную в трехмерное пространство, можно покрыть дисками, то ее a fortiori можно покрыть шарами, экваторами которых являются эти диски. Следовательно, если мы не хотим заранее считать множество S плоским, нам достаточно покрыть его вместо дисков шарами. Если же S и в самом деле является поверхностью, ее приближенную меру можно получить простым сопоставлением каждому шару выражения вида πρ 2 и последующим сложением этих выражений. В более общем виде, для получения меры какой-либо d - мерной фигуры следует складывать выражения вида h(ρ)=γ(d)ρ d ; входящая сюда функция γ(d)=[Γ(1/2)] d/Γ(1+d/2) была определена ранее в этой главе как протяженность шара единичного радиуса. На этом основании Каратеодори [67] распространяет понятия «длины» и «площади» и на нестандартные фигуры.

Хаусдорф [203] расширяет определение Каратеодори, допуская возможность дробного значения d (функция γ(d) записывается таким образом, что она при этом продолжает иметь смысл). Таким образом, мы больше не ограниченны степенями ρ , а вольны использовать любую положительную пробную функцию h(ρ) , которая стремится к нулю вместе с ρ .