Бенуа Мандельброт - Фрактальная геометрия природы

Более того, поскольку шар представляет собой всего лишь множество точек, расстояние до которых от центра w не превышает заданного радиуса ρ , шар продолжает оставаться определенным даже в случае неевклидова пространства Ω - при условии, что в этом пространстве определено расстояние. Как мы уже отмечали, такие пространства называются метрическими, следовательно, и хаусдорфова мера представляет собой метрическое понятие.

Если задана некоторая пробная (или «калибровочная») функция h(ρ) , то можно сказать, что мера конечного покрытия множества S шарами радиуса ρ m равна ∑h(ρ m) . Для получения наиболее экономичного покрытия мы рассматриваем все покрытия шарами, радиус которых меньше ρ , и образуем инфимум

.

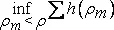При ρ→0 ограничение ρ m <���ρ становится чрезвычайно жестким. То есть выражение inf∑h(ρ m) может только возрастать; у него есть предел, который имеет вид

.

Этот предел может быть конечным положительным, отрицательным или нулевым. Он определяет h - меру множества S .

Если h(ρ)=γ(d)ρ d , то h - мера называется d - мерной. Точнее говоря, из-за префактора γ(d) h - мера является нормированной d - мерной мерой.

Если h(ρ)=1/ln|ρ| , то h - мера называется логарифмической.

Функцию h(ρ) можно назвать внутренней для множества S и обозначить как h S (ρ) , если h S - мера S положительна и конечна. Эту меру можно назвать фрактальной мерой множества S .

Для стандартных фигур евклидовой геометрии внутренняя пробная функция всегда имеет вид h S (ρ)=γ(D)ρ D , где D - некоторое целое число. Хаусдорф показал, что внутренней для канторовых пылей и кривых Коха является функция h S (ρ)=γ(D)ρ D с нецелочисленным значением D .

Типичные случайные фракталы, пусть даже и статистически самоподобные, также обладают внутренней функцией h S (ρ) , однако она имеет более сложный вид – например, h S(ρ)=ρ Dln|ρ| . В этом случае h - мера множества S относительно функции h(ρ)=γ(D)ρ D обращается в нуль, т.е. фигура содержит меньше «вещества», чем если бы она была D - мерной, но больше, чем если бы она была D - ε -мерной. В качестве примера можно привести траекторию броуновского движения на плоскости, внутренняя функция для которого, согласно Леви, имеет вид h(ρ)=ρ 2ln ln(1/ρ) . См. [560].

Поскольку двумерная мера любого ограниченного множества на плоскости конечна, пробные функции вида ρ 2 / ln (1/ρ) не могут быть внутренними ни для какого плоского множества.

Автором (либо соавтором) многих работ, посвященных определению внутренних функций h S (ρ) случайных множеств, является С. Дж. Тейлор; особо рекомендую обратить внимание на статью [484] (написанную им в соавторстве с У. Э. Прюиттом).

Если известно, что множество S двумерно, вполне достаточно оценить хаусдорфову h - меру для h(ρ)=πρ 2 . Однако определение хаусдорфовой меры сформулировано таким образом, что предварительного знания размерности D не требуется. Имея дело со стандартной фигурой неизвестной размерности, мы будем оценивать ее меру для всех пробных функций h(ρ)=γ(d)ρ d , где d - целое число. Если длина фигуры бесконечна, а объем равен нулю, то она может быть только двумерной.

Безикович распространил суть последнего заключения на случаи, в которых показатель d не является целым числом, а множество S - стандартной фигурой. Он показал, что для каждого множества S существует такое вещественное значение D , что d - мера этого множества при d бесконечна, а при d>D обращается в нуль.

Эта величина D и называется размерностью Хаусдорфа – Безиковича множества S .

Для физика это означает, что величина D представляет собой критическую размерность.

D - мерная хаусдорфова мера D - мерного множества S может быть либо равна нулю, либо бесконечна, либо положительна и конечна. Хаусдорф ограничился только последним, самым простым, случаем и показал, что в эту категорию входят канторовы множества и кривые Коха. Если множество S ко всему прочему еще и самоподобно, легко заметить, что его размерность подобия должна быть равна D . С другой стороны, мы знаем, что типичные случайные множества имеют в качестве естественной размерности нулевую меру.

Долгое время Безикович являлся автором или соавтором почти всех публикуемых по данной теме работ. Если Хаусдорфа можно назвать отцом нестандартной размерности, то Безикович, несомненно, заслужил себе звание ее матери.

Коразмерность.Когда в роли пространства Ω выступает ℝ E , D≤E , а разность называется коразмерностью.

Рассмотрим множества S 1 и S 2 , принадлежащие, соответственно, E 1 - пространству и E 2 - пространству, и обозначим через S множество в E - пространстве (E=E 1 +E 2 ) , представляющее собой произведение множеств S 1 и S 2 . (Если E 1 =E 2 =1 , то S - это множество расположенных на плоскости точек (x,y) , причем x∈E 1 и y∈E 2 .)

Эмпирическое правило гласит, что если множества S 1 и S 2 «независимы», то размерность множества S равна сумме размерностей множеств S 1 и S 2 .

Понятие «независимости», входящее в это правило, оказывается неожиданно сложно сформулировать и представить в общем виде. См. [413, 414], [204] и [416]. К счастью, в подобных прецедентных исследованиях (в таких, например, какие мы рассматриваем в настоящем эссе) нас, как правило, спасает интуиция.

Эмпирическое правило выглядит следующим образом: если S 1 и S 2 суть независимые множества в E - пространстве, и