Бенуа Мандельброт - Фрактальная геометрия природы

Рис. 106, слева.Четвертый терагон кривой Госпера, перерисованный в виде границы между черной и белой областями.

Рис. 106, справа. Деревья рек и водоразделов.Изображены реки и водоразделы, проходящие по средним линиям черных и белых «пальцев» кривой, показанной на этом же рисунке слева.

Рис. 107, вверху.Мы взяли древовидную структуру рек и водоразделов, показанную на рис. 106 справа, и привели толщину линий в соответствие с их относительной значимостью в схеме Хортона-Штралера (см. [297]). В настоящем примере каждой кривой (и рекам, и водоразделам) назначается ширина, пропорциональная ее длине по прямой. Реки даны черным, водоразделы — серым.

Размерности.Каждая кривая Пеано определяет размерность D собственной границы. На рис. 95 и 98 указанная граница представляет собой просто квадрат. На последующих рисунках появляются драконова шкура и кривая-снежинка. Здесь же мы имеем дело с фрактальной кривой, размерность которой D~1,1291 и которая состоит отчасти из рек, отчасти из водоразделов. Все другие реки и водоразделы сходятся к кривой с фрактальной размерностью D=1,1291 .

Франция.Тому, кто, будучи школьником, часто разглядывал карту бассейнов Луары и Гаронны, наши иллюстрации наверняка о многом напомнят.

Рис. 107, внизу. Дерево рек, построенное непосредственно с помощью каскада Коха.Когда сам генератор имеет древовидную структуру, он порождает при построении дерево. Пусть, например, генератор выглядит вот так:

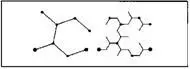
Получаем еще один способ осушения внутренней области кривой Коха с рис. 75. (Ветви, расположенные у самых «истоков», были обрезаны.)

Заполняющие плоскость «речные» деревья, получаемые из некоторых кривых Пеано, могут быть получены и с помощью прямого рекурсивного построения. Ключом здесь служит генератор, который сам имеет древовидную форму. Простейший и скучнейший пример: генератор составлен из четырех отрезков, образующих фигуру, похожую на знак «+». В результате построения получим речное дерево кривой Пеано- Чезаро (см. рис. 99).

Перекошенная снежинка.Более интересного результата можно достичь, взяв в качестве инициатора отрезок [0, 1], а в качестве генератора — следующую фигуру:

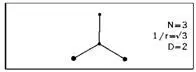
Для начала обратим внимание на то, что отдельные реки порождаются генератором, который смещает среднюю точку отрезка (таким, например, как на рис. 71). Следовательно, всякая асимптотическая река имеет размерность D= ln2 / ln√3 = ln4 / ln3. Это значение хорошо знакомо нам еще по снежинке Коха, однако кривая, которой мы намерены заняться теперь, — не снежинка, поскольку размещение генератора на прямолинейных отрезках следует иному правилу.

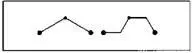
Если мы хотим, чтобы осталось место для рек, необходимо, чтобы положение генератора с каждым отрезком менялось с правого на левое и наоборот. Таким образом симметрия снежинки искажается, а новая область для заполнения реками заслуживает себе имя — перекошенная снежинка.

Вернемся к дереву рек. Его терагоны не перекрывают сами себя, но самокасаний здесь очень много. Неизбежен — и даже напрашивается — асимптотический вариант этой особенности, поскольку он вполне верно отражает тот факт, что иногда несколько рек начинаются в одной точке. Как мы увидим чуть позже, речные терагоны могут и вовсе обходиться без самокасаний. Рассматриваемый же речной терагон — как раз благодаря самокасаниям — представляет собой ({- неразборчиво заштрихованный обрывок гексагональной диаграммной бумаги в форме близкой фрактальной кривой.

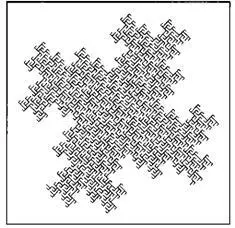
Рис. 110, вверху.Речное дерево станет более явным, если стереть все участки реки, соприкасающиеся с истоком, и изобразить главную реку более жирной линией. Площадь бассейна такой реки составляет √ 3/2~0,8660 .

Прохождение перекошенной снежинки.Построим кривую Пеано, инициатор которой имеет форму равностороннего треугольника, а генератор представляет собой ломаную линию, звенья которой равны и расположены под углом в 60° друг к другу. Это — крайний случай при M=3 из семейства генераторов, использованных при построении кривых на рис. 75 и 76, причем он значительно отличается от остальных случаев этого семейства. Подробнее см. в [95].

Можно легко убедиться, что дерево рек этой кривой Пеано совпадает с деревом, которое мы только что получили с помощью прямого построения. Длина стороны инициатора равна 1, а площадь, заполняемая соответствующей кривой Пеано, составляет √ 3/6~0,2886 (очень неэффективно!).

Квартет.Теперь рассмотрим другую кривую Коха вместе с тремя кривыми, заполняющими ее: одной кривой Пеано и двумя деревьями. Эти придуманные мною фигуры иллюстрируют еще одну весьма интересную тему.

Инициатором снова будет отрезок [0, 1], а генератор выглядит следующим образом:

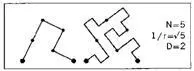
Граница заполняемой области стремится в пределе к кривой Коха с размерностью D= ln3 / ln√5 =1,3652 . Продвинутые терагоны границы и кривой Пеано составляют центр рис. 79; я назвал эту фигуру квартетом. Каждый «игрок», равно как и стол между ними, способен к самоподобному разбиению плоскости.

Внутренняя область квартета заполняется, конечно же, и его собственным деревом рек. Однако если воспользоваться каким-либо из следующих генераторов, можно получить совершенно другие варианты заполнения:

Терагоны, построенные с использованием левого генератора, демонстрируют самокасания (как и кривые в первом примере данного пояснения). Заполняемая площадь составляет 1/2. Правый генератор позволяет терагонам избежать самокасаний, и заполняемая площадь увеличивается до 1. На рис. 110 (внизу) показан один из продвинутых терагонов такой кривой.