Бенуа Мандельброт - Фрактальная геометрия природы

Обратите внимание также на то, что для любого D<1 есть по крайней мере одно канторово множество, однако поскольку Nr≤1 и, как следствие, N≤1/r , нет ни одного множества, размерность D которого превышала бы 1.

Фрактальная размерность D канторова множества может изменяться в пределах от 0 до 1; с топологической же точки зрения все канторовы множества имеют размерность 0, так как, по определению, любая точка канторова множества отделена от любой другой, причем для ее отделения не требуется ничего удалять. С этой стороны нет никакой разницы между C и конечным множеством точек! Тот факт, что топологическая размерность D T в последнем случае равна 0, известен нам из стандартной геометрии; мы даже используем это обстоятельство в главе 6 для доказательства того, что топологическая размерность кривой Коха K равна 1. Вообще, D T =0 для любого вполне несвязного множества.

При отсутствии общепринятого обыденного термина, вроде «кривой» и «плоскости» (которые представляют собой связные множества с размерностями D T =1 и D T =2 , соответственно), я предлагаю называть множества с D T =0 пылью.

Возьмем канторову пыль и обозначим через и возможное значение для длины паузы, через U — неизвестную длину паузы, а через Nr(U>u) — количество пауз или трем длины U , большей, чем u . < Это обозначение построено по аналогии с обозначением Pr(U>u) из теории вероятности. ► Оказывается, существует постоянный префактор F — такой, что график функции Nr(U>u) постоянно пересекает график Fu −D . И вновь в дело вступает размерность. Приняв за координаты ln u и ln Nr , получим однородные ступени.

Как и в случае береговых линий, можно получить приблизительное представление о последовательности ошибок, если остановить канторо- во створаживание при длине интервалов ε=3 −k . Эта величина может быть равна времени, необходимому для передачи единичного символа. Кроме того, следует использовать канторову периодическую экстраполяцию с большим, но конечным значением Ω .

Количество ошибок между моментами времени 0 и R (которое мы обозначим через M(R) ) выдерживает ритм, так как учитываются только те моменты, в которые происходит что-то важное. Хороший пример фрактального времени.

Если сигнал начинается в момент времени t=0 (а мы рассматриваем только этот случай), величина M(R) ведет себя так же, как в случае кривой Коха. Пока R остается меньше 0, количество ошибок удваивается всякий раз, когда R увеличивается в 3 раза. В результате имеем M(R)∝R D .

Это выражение похоже на стандартное выражение для массы диска или шара радиуса R в D -мерномевклидовом пространстве. Оно также идентично выражению, полученному в главе 6 для кривой Коха.

В качестве вывода можно заметить, что среднее количество ошибок на единицу длины приблизительно пропорционально R D−1 при условии, что R находится в интервале между внутренним и внешним порогами. При конечном Ω уменьшение среднего количества ошибок продолжается до окончательной величины Ω D−1 которая достигается при R=Ω . После этого их плотность остается более или менее постоянной. При бесконечном Ω среднее количество ошибок уменьшается в конечном счете до нуля. Наконец, эмпирические данные часто предполагают, что величина Ω конечна и очень велика, однако не позволяют определить ее со сколько-нибудь приемлемой точностью. В этом случае среднее количество имеет некоторый нижний предел, который не обращается в нуль, но его неопределенность лишает его какого бы то ни было практического смысла.

< Наиболее заметные члены множества C , концевые точки трем, вовсе не исчерпывают всего множества; скажем больше, они составляют лишь малую его часть. Физическую значимость других точек мы обсудим в главе 19. ►

Читателю, который продержался до этого места и/или/ наслышан об активно сейчас обсуждаемых в научной литературе чертовых лестницах (см. пояснение к рис. 125), возможно, будет сложно поверить в то, что, когда я начал работу над этой темой в 1962 г., все вокруг были единодушны в том, что канторова пыль по меньшей мере столь же чудовищна, как кривые Коха и Пеано.

Каждый уважающий себя физик автоматически «выключался» при одном только упоминании имени Кантора, порывался убежать за тридевять земель от всякого, заявляющего о научной ценности множества C , и всех желающих слушать с готовностью уверял в том, что все подобные заявления были приняты, рассмотрены и найдены беспочвенными. Поддержали меня в то время только предположения С. Улама (совершенно завораживающие, несмотря на отсутствие должной проработки и неприятие научной общественностью) относительно возможной роли канторовых множеств при изучении гравитационного равновесия в звездных скоплениях (см. [570]).

Чтобы опубликовать работу о канторовой пыли, мне пришлось убрать из нее всякое упоминание имени Кантора!

Однако случилось так, что Природа сама привела нас к множеству C . В главе 19 мы поговорим еще об одной, совершенно иной, физической роли для C . Все это призвано подчеркнуть, что истинная природа канторовой пыли весьма разнообразна.

Несомненно, в большинстве случаев само множество C представляет собой весьма грубую модель, нуждающуюся в многочисленных уточнениях. И все же я настаиваю, что те самые свойства, благодаря которым многие считают канторовы дисконтинуумы патологией, незаменимы при моделировании перемежаемости и должны быть сохранены в последующих, более реалистичных, заменителях этих множеств.

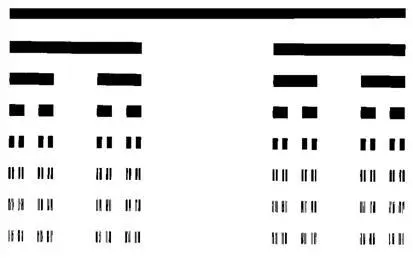
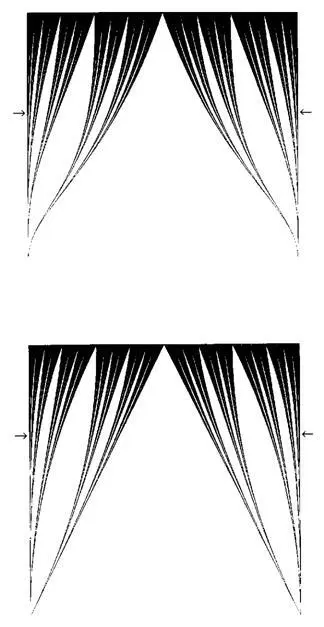
Рис. 120 и 121. КАНТОРОВЫ ТРОИЧНЫЕ ГРЕБЕНЬ И БРИКЕТ (РАЗМЕРНОСТЬ ГОРИЗОНТАЛЬНОГО СЕЧЕНИЯ D= ln2 / ln3 =0,6309 ). КОЛЬЦА САТУРНА. КАНТОРОВЫ ЗАНАВЕСЫ

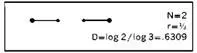
Инициатором для канторовой пыли служит интервал [0, 1], а генератор имеет следующий вид: