Бенуа Мандельброт - Фрактальная геометрия природы

Приращения персистентны, и график функции B H (t) менее иррегулярен, чем график обыкновенной броуновской функции B(t) , причем во всех масштабах. Это выражается в размерности функции B H (t) ( D=2−H ). Размерность ее нуль – множества равна 1−H .

В случае двумерной векторнозначной функции B H (t) нас будут интересовать движения, направления которых стремятся персистентности во всех масштабах. Персистентность включает в себя достаточно сильное стремление (не подразумевающее, однако, обязательности) избежать самокасаний. А поскольку в настоящем Эссе мы желаем сохранить и самоподобие, допустим, что координатные функции X H (t) и Y H (t) представляют собой дробные броуновские функции из прямой в прямую от времени, статистически независимые и характеризующиеся одним параметром H . Таким образом, мы получаем дробный броуновский след из прямой в плоскость (см. рис. 357).

Фрактальная размерность такого следа определяется как D=1/H ; ее наименьшее значение D=1/1=1 , каким оно, собственно, и должно быть у кривой, а наибольшее - D=1/(½)=2 . Последнее значение предполагает, что след функции B H (t) заполняет плоскость менее «плотно», чем обыкновенный броуновский след. Для того чтобы подтвердить это предположение, рассмотрим по отдельности ограниченный и неограниченный следы.

Влияние параметра H на ограниченные следы носит чисто количественный характер. При H>½ (равно как и при H=½ ) ограниченный броуновский след представляет собой фрактальную сеть, пронизанную бесконечным количеством пустот. Исходя из сильных эвристических соображений, можно предположить, что площадь этих пустот удовлетворяет равенству Pr(U>u)∝u −D/E=u 1/2H .

Кроме того, я экспериментально исследовал границы ограниченных следов с различными D в поисках отклонения от значения 4/3 , каковое значение, согласно пояснению к рис. 340, наблюдается в броуновском случае. Никакого сколько-нибудь явного отклонения я не обнаружил!

На неограниченные же следы параметр H оказывает качественное влияние. Если след начинается в точке O в момент времени 0, то известно, что ожидаемое количество его возвращений в малую окрестность точки O бесконечно для броуновской модели; однако при H>½ оно становится конечным. Причина заключается в том, что интеграл 1∫ ∞t −2Hdt , полученный в предпоследнем разделе главы 25, при H=½ расходится, а при H>½ сходится. Когда в одном объеме укладывается некоторое конечное число фрактальных сетей, покрытие становится менее лакунарным, однако достичь таким образом плотного покрытия почти наверное невозможно. Количество уложенных в одном объеме решеток мало, если значение параметра H близко к 1, и устремляется к бесконечности при H=½ .

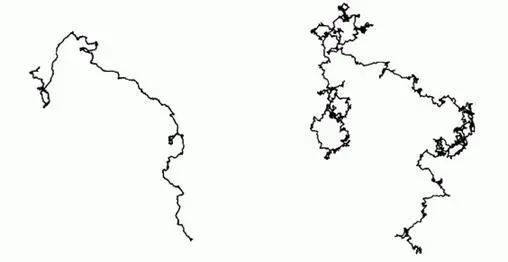
Рис. 357 Дробные броуновские следы (размерности D~1,1111 и D~1,4285 )

На рисунке слева представлен пример статистически самоподобной фрактальной кривой с размерностью D=1/0,9000~1,1111 . Ее координатные функции – независимые дробные броуновские функции с показателем H=0,9000 , которым и обусловлено возникновение на Ниле эффекта Иосифа. Того обстоятельства, что H близок к 1, оказывается недостаточно для предотвращения самопересечений, однако оно весьма осложняет им существование, побуждая «тренд» кривой к персистентности в любом направлении, какое он уже избрал. Представляя сложные кривые как наложения друг на друга больших, средних и малых сверток, можно сказать, что в случае высокой персистентности и близости размерности к единице малые свертки едва различимы.

Для рисунка справа мы воспользовались той же компьютерной программой, что и для рисунка слева, изменив лишь размерность D (теперь она равна D=1/0,7000~1,4285 ). Псевдослучайная затравка не изменилась, поэтому общая форма линии остается узнаваемой. Однако увеличение D приводит к росту относительной значимости малых сверток, а также – до некоторой степени – и средних. Становятся отчетливо видны ранее невидимые детали.

Дробные броуновские движения с 0 описываются антиперсистентными функциями и следами. Под антиперсистентностью подразумевается стремление постоянно возвращаться к исходной точке, следствием чего является более медленное (чем у броуновских аналогов) рассеяние.

Формула D=1/H справедлива только при условии, что E>1/H . Если же E<1/H (особенно в случае плоскости, E=2 ), то фрактальная размерность достигает наибольшего возможного значения, D=E . Напомним, что наибольшим возможным значением размерности для броуновского следа является D=2 , и этот максимум может быть реализован только в случае E≥2 . Если втиснуть броуновский след в реальную прямую с размерностью E=1 , то ему придется примириться с D=1 . При H=⅓ след ДБД едва заполняет обыкновенное З – пространство.

В случае же плоскости (E=2) анализ размерностей показывает, что неограниченный след с H<���½ почти наверное посещает любую заданную точку бесконечно часто. Таким образом, в противоположность функции B(t) , которая не совсем отвечает ожиданиям, связанным с ее размерностью D=2 , и заполняет плоскость плотно, но не полностью, броуновский след при любом превышении параметром 1/H значения 2 заполняет плоскость полностью. Для доказательства того, что след B H (t) почти наверное бесконечно часто возвращается к своей исходной точке, вспомним из главы 25, что размерность множества моментов возвращения равна 1−2H и, как следствие, при H<���½ положительна. Это же рассуждение справедливо и для точек, отличных от O . Следовательно, пересечение неограниченного дробного броуновского следа при H<���½ с единичным квадратом имеет единичную же площадь.

Ограниченный след представляет собой сеть с пустотами, однако площадь его положительна (привет из главы 15!).

Нужно заметить, что первоначальная мотивировка введения функции B H основана на личном опыте пишущего эти строки геометра, чьи математические и графические приемы, как правило, срабатывают. Я готов поспорить, что отсутствие серьезной мотивировки в модели, которая согласуется с явлением и должным образом работает, гораздо предпочтительнее, нежели недостаток согласованности в модели, которая выглядит хорошо мотивированной; однако ученым подавай и то, и другое. К сожалению, существующие «объяснения» несколько, на мой взгляд, надуманны и еще менее ясны, чем само объясняемое явление.