Бенуа Мандельброт - Фрактальная геометрия природы

Из-за того, что нуль - множества периодичны и синхронны («иерархичны»), приращения не могут быть стационарными. И наоборот, стационарности можно достичь путем устранения этих свойств.

Один из подходов состоит в построении ломаной функции ΔB k f(t) следующим образом. Выберем пуассоновскую последовательность моментов времени t n (k) со средним числом точек на единицу времени, равным 2 k , затем положим, что функция 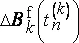принимает независимые и одинаково распределенные случайные значения, и, наконец, произведем линейную интерполяцию между моментами времени t n (k) . Бесконечная сумма B H f(t) таких вкладов представляет собой некую стационарную случайную функцию, впервые описанную в докторской диссертации гидролога О. Дитлефсена (1969). (См. также [424] и [370].)

Оглянувшись назад, мы видим, что такое обобщение вовсе не требует, чтобы среднее число нулей было равно 2 k . Оно может иметь вид b k , где b - любая вещественная база, большая 1.

Допустимые отношения приведения соответствующего фрактала задаются дискретной последовательностью r=b −k . По мере того, как b→1 , эта последовательность становится все более плотной, - в сущности, асимптотически непрерывной. Таким образом, функция B H f(t) становится как нельзя более приемлемой для тех, кому нужны стационарность и широкий выбор коэффициентов подобия. Однако при этом она, к сожалению, теряет свою специфичность. Из рассуждений в [370] явствует, что функция B H f(t) сходится к случайной функции B H (t) , которую мы рассмотрим в следующей главе.

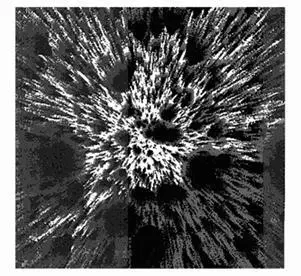
Рис. 345. В роли художника – ошибка в программе, опус 1

Авторство этой иллюстрации можно частично приписать ошибочному программированию. Ошибку вовремя распознали и исправили (после сохранения результата, разумеется!); конечным результатом вы можете полюбоваться на рис. 424 – 427.

Изменения, явившиеся результатом пустяковой ошибки в критическом месте, далеко превзошли наши наихудшие опасения.

Очевидно, что по замыслу в «правильных» иллюстрациях должен был наличествовать весьма строгий порядок. Здесь этот порядок оказался нарушен, причем никакого другого порядка также не наблюдается.

То, что эта иллюстрация – по крайней мере, на первый взгляд, - вполне может сойти за произведение высокого искусства, явно не случайно. Свои соображения на этот счет я вкратце высказал в [399] и намерен изложить их в полном виде в самом ближайшем будущем.

Переход к дробным броуновским фракталам знаменует собой один из важнейших поворотных пунктов настоящего эссе. До сих пор мы придерживались фракталов, связанных с временными и/или/ пространственными решетками, которые налагали определенные ограничения на свойства инвариантности фракталов, т.е. на допустимые преобразования сдвига и подобия, отображающие данный фрактал на себя.

Такие ограничения противоречат второму доводу в пользу рандомизации фракталов, изложенному в главе 22. Более того, в большинстве занимающих нас случаев они не имеют никакого физического смысла. И вот теперь, в главах 27 – 35, мы займемся, наконец, фракталами, инвариантности которых и при сдвиге, и при преобразовании подобия остаются ничем не ограниченными.

В этой главе мы рассмотрим обобщенное броуновское движение (обозначив его через B H (t) ), которое в [404] называется дробным броуновским движением (сокращенно, ДБД). В качестве мотивации здесь выступит необходимость отыскания закономерности изменения объемов годового стока рек, а кроме того, упоминаются масштабно-инвариантные сети и шумы (« 1/f - шумы). Главы 28 – 30 посвящены исследованию соответствующих поверхностей.

Первой чертой, объединяющей главы 27 – 30, является то, что все они занимаются исключительно гауссовыми процессами. Статистики полагают, что «гауссовость» непременно представляет собой нечто чрезвычайно особенное, однако я с некоторых пор не разделяю эту точку зрения. (см. мои замечания по этому поводу в главе 42.) Тем не менее, гауссовы процессы остаются своего рода эталонным тестом, и их следует изучить прежде, чем мы начнем двигаться дальше.

Еще одна присущая главам 27 – 30 особенность не встречается ни в каком другом месте настоящего эссе.

Конструкции (и случайные, и нет), описываемые в других главах, строятся рекурсивно, т.е. посредством добавления все более мелких деталей к менее детализированным формам, полученным на предыдущих этапах построения. Свойства получающегося при этом фрактала выводятся из правил построения.

Теперь же мы начинаем с объявления желательными тех или иных свойств и только затем находим такие правила построения, которые удовлетворяли бы нашим пожеланиям. Хотя искомые свойства легко формулируются и выглядят простыми, реализующие их правила, к сожалению, нерекурсивны и, более того, часто весьма неприятны.

Если все так плохо, то почему же мы продолжаем настаивать на этих свойствах? Потому что в их число входят такие свойства, как самоподобие и отсутствие складок (т.е. стационарность), составляющие самую суть науки вообще и теории фракталов, в частности.

Относительная ценность «аксиоматического» подхода, используемого в этой главе, видна особенно отчетливо, когда его результат сравнивается с фракталом, полученным рекурсивно. Представьте себе, например, что вы исследуете какой-то конкретный случай, требующий построения плоской фрактальной кривой, размерность D которой лежит где-то между 1 и 2, и не можете решить, какой метод для этого использовать: процесс срединного смещения из главы 26 или процесс, описываемый ниже. В первом неизбежны складки, тогда как второй лишен этого недостатка. А последовательность дискретных этапов, из-за которой рекурсивные построения представляются столь привлекательными, оборачивается в большинстве случаев возникновением слоев, не имеющих никакого смысла, а зачастую и вовсе нежелательных.

Прозвучавшее в первой главе утверждение о том, что негладкие природные структуры издавна привлекали внимание людей, как правило, очень трудно подтвердить документально. Однако в Библии имеются два совершенно очаровательных исключения из этого правила: