Бенуа Мандельброт - Фрактальная геометрия природы

Раз уж мы управляем лакунарностью линейной пыли, мы вполне можем отобразить результат на пространство с помощью процесса субординации, описанного в главе 32. Имея дело с плоскостью и используя в качестве субординанда броуновскую сеть (см. рис. 341), можно построить пыль, которая произвольно близка к тому, чтобы выглядеть как сеть, и характеризуется бесконечной степенью ветвления. Начнем с плоскости и положим, что субординанд представляет собой дробную броуновскую сеть с H>½ ; пустоты такой сети имеют меньший размер, чем пустоты сети с H=½ . Если при этом размерность субординатора удовлетворяет неравенству D/H , а лакунарность субординатора низка, то можно добиться того, что субординат будет произвольно близок к тому, чтобы казаться заполняющим плоскость. В случае E=3 и H=⅓ субординанд является заполняющей пространство кривой. Если D/H , а лакунарность субординатора низка, то можно добиться того, что субординатная пыль будет заполнять пространство; при этом степень ее лакунарности может быть сколько угодно низкой, независимо от величины D .

Рис. 446. Влияние трема – генератора на лакунарность трема — фрактала

Эти иллюстрации призваны дать читателю представление о степени влияния формы трема – генератора на лакунарность фрактала. Оба трема – генератора имеют форму ромба, однако первый ромб представляет собой почти квадрат, а второй больше похож на тонкую иглу. Внутри белых областей можно разглядеть отдельные маленькие черные ромбы.

Оба построения характеризуются одинаковой размерностью D ; площади наибольшего и наименьшего ромбов также одинаковы. Отсюда следует, что в обоих случаях одинаковы и площади оставшихся белыми областей (с учетом статистической изменчивости). Тем не менее, непосредственное наблюдение со всей очевидностью свидетельствует о том, что белые участки на одном из рисунков распределены гораздо более равномерно, чем на другом. В соответствии с введенными мною мерами лакунарности более равномерно распределенные белые остатки характеризуются более низким значением коэффициента лакунарности.

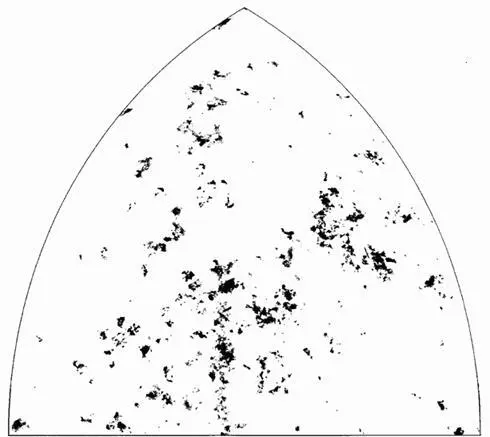
Рис. 447. Фрактальная пыль, получаемая при использовании несферических трем:

Проекция одного пространственного октанта на сферический небосвод

Мне, право, очень неловко об этом говорить, но изначально я планировал поместить здесь совсем другую иллюстрацию, и более того - в настоящий момент я не в состоянии припомнить точных спецификаций той, которая все-таки сюда попала. Причина весьма незамысловата. К первому января 1979 г. мы подготовили огромное количество изображений фракталов с размерностью D~1,23 и различными степенями лакунарности и сукколяции. Бóльшая часть готовых иллюстраций хранилась в одной папке, которую куда-то засунули и не смогли потом отыскать; к счастью, в других папках уцелели некоторые предварительные результаты, однако ярлыки к ним оказались никуда не годными. Времени на повторный запуск программы уже не оставалось, поэтому пришлось довольствоваться тем, что удалось спасти.

Насколько я помню, построение для данной иллюстрации начинается с периодической структуры, периодом которой является кубическая решетка 600×600×600 . Иными словами, вычисление проводится на решетке 600×600×600 , противоположные грани которой совпадают, образуя тор. Распределение объемов трем усечено. Поскольку тремы в процессе построения удаляются, точка начала координат перемещается в некоторую не удаленную точку, которая выбирается либо произвольно, либо внутри области с высокой плотностью.

Точки, близкие к началу координат, исключаются из результата построения, остальные же сортируются по оболочкам, задаваемым неравенством R 1 22+y 2+z 22 2 , в соответствии с уменьшающимся уровнем яркости. Каждая оболочка проецируется на сферический небосвод.

Целью построения является обработка имеющихся в наличии данных с тем, чтобы извлечь из них максимальное количество независимой информации. При малых значениях R 2 можно составить карту всего небосвода целиком, однако при бóльших R 2 не следует обрабатывать больше некоторой разумной доли одного периода исходной периодической структуры. Максимальное значение R 2 в самой внешней оболочке соответствует карте, ограниченной одним-единственным октантом небесной сферы – например, областью, где x>0, y>0 и z>0 . Определяя этот октант в сферических координатах, можно сказать, что он соответствует положительным значениям широты (северное полушарие), долгота же при этом варьируется от − 45° до 45° . В использованной здесь хаммеровской проекции этот октант отображается на участок, напоминающий готическое стрельчатое окно; см. нижеследующий рисунок.

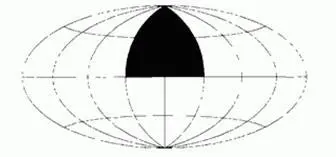
Когда R 2 достигает 600, данные в окрестностях трех вершин становятся статистически зависимыми, причем окрестности нижних вершин, лучше всего, совсем исключить из рассмотрения. Таким образом, данные за пределами R 2 =600 , а также данные в окрестностях точек x=z=0 , y=600 и y=z=0 , x=600 , приходится принести в жертву необходимости избежания статистической зависимости, порождаемой периодичностью. С другой стороны, для построения небосвода для антиподов ( x<0, y<0 и z<0 , т.е. южные широты и долготы θ , удовлетворяющие неравенству |θ−180°|<45° ) не требуется заново проводить вычисления, а результат может оказаться достаточно отличным от предыдущего, и его вполне можно будет рассматривать как источник дополнительной информации.

На заключительном этапе обработки, целью которого является уничтожение следов исходной кубической решетки, все точки смещаются вдоль векторов, координаты которых равномерно распределены на интервале [0,1]. К сожалению, в результате этой процедуры образуются сплошные серые участки различной степени насыщенности, которые искажают получаемую фрактальную пыль: мы видим не что иное, как сглаженные версии областей с высокой степенью неравномерности.

На представляемой вниманию читателя иллюстрации R 2 =600 , а R 1 =R 2 /1,5 , т.е. модули векторов лежат в узком диапазоне, ширина которого равна 2,5lg(1,5) 2 ~0.88 .